Derive an expression for one dimensional simple harmonic progressive wave travelling in the
direction of positive X-axis. Express it in ‘two’ different forms.
Solution
Equation of simple harmonic progressive wave:
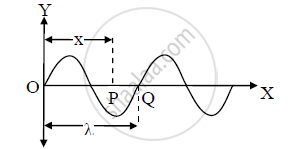
a) Consider a simple harmonic progressive wave travelling in the direction of the positive X-axis. The vibrations of the particles of the medium is parallel to the Yaxis.
b) At time t = 0, particle is at origin O i.e., the mean position. At instant ‘t’,
displacement of the particle is,
y = A sin ωt ….(i)
where, A = amplitude,
ω = angular velocity
c) Consider a particle P situated at a distance ‘x’ from O. If ‘δ’ be the phase difference between the particle P and O, then displacement of the particle of the medium at P in instant ‘t’ is given by,
y = A sin (ωt − δ) .…(ii)
d) A path difference of λ between two particles of a medium corresponds to a phase difference of 2π between them (e.g. particle O and Q). Since the path difference between P and O is ‘x’, so the phase difference ‘δ’ between them is given by,
`δ = (2pix)/lambda` ....(iii)
Substituting equation (iii) in equation (ii) we have
`y = A sin[ωt - (2pix)/lambda]` ....iv
This equation gives the displacement of any particle of the medium at any instant. Hence, it is called equation of a simple harmonic progressive wave.
e) Since
All the above equations represent one-dimensional simple harmonic progressive wave,
travelling in the direction of the positive X-axis.
