Question

Draw a ray diagram for the formation of the image of a point object by a thin double convex lens having radii of curvature R₁ and R₂. Hence derive lens maker’s formula.

Answer 1

Lensmaker’s Formula:

When a ray refracts from a lens (double convex), in the above figure, then its image formation can be seen in terms of two steps:

Step 1: The first refracting surface forms the image l₁ of the object O.

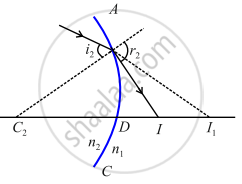
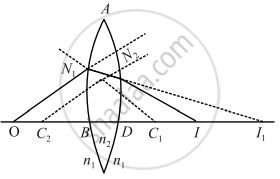
Step 2: The image of object O for the first surface acts like a virtual object for the second surface. Now for the first surface ABC, the ray will move from a rarer to a denser medium, and then

`n_2/(BI_1) + n_1/(OB) = (n_2 - n_1)/(BC_1)`   ...(i)

Similarly for the second interface, ADC we can write.

`n_1/(DI) - n_2/(DI_1) = (n_2 - n_1)/(DC_2)`   ...(ii)

DI₁ is negative as the distance is measured against the direction of incident light.

Adding equation (1) and equation (2), we get

`n_2/(BI_1) + n_1/(OB) + n_1/(DI) - n_2/(DI_1) = (n_2 - n_1)/(BC_1) + (n_2 - n_1)/(DC_2)`

Or `n_1/(DI) + n_1/(OB) = (n_2 - n_1)(1/(BC_1) + 1/(DC_2))`   ...(iii) (∵ for the thin lens BI₁ = DI₁)

Now, if we assume the object to be at infinity i.e. OB → ∞, then its image will form at focus F (with focal length f), i.e.

DI = f, thus equation (iii) can be rewritten as:

`n_1/f + n_1/∞ = (n_2 - n_1)(1/(BC_1) + 1/(DC_2))`

or `n_1/f = (n_2 - n_1)(1/(BC_1) + 1/(DC_2))`   ...(iv)

Now according to the sign conventions,

BC₁ = +R₁ and DC₂ = -R₂    ...(v)

Substituting equation (v) in equation (iv), we get

`n_1/f = (n_2 - n_1)(1/R_1 - 1/R_2)`

`1/f = (n_2/n_1 - 1)(1/R_1 - 1/R_2)`

`1/f = (n_{21} - 1)(1/R_1 - 1/R_2)`