Advertisements
Advertisements
प्रश्न
A, B and C can reap a field in \[15\frac{3}{4}\] days; B, C and D in 14 days; C, D and A in 18 days; D, A and B in 21 days. In what time can A, B, C and D together reap it?
उत्तर
\[\text{ Time taken by } \left( A + B + C \right) \text{ to do the work } = 15\frac{3}{4} \text{ days } = \frac{63}{4} \text{ days } \]
\[\text{ Time taken by } \left( B + C + D \right) \text{ to do the work = 14 days} \]
\[\text{ Time taken by } \left( C + D + A \right) \text{ to do the work = 18 days } \]
\[\text{ Time taken by } \left( D + A + B \right) \text{ to do the work = 21 days } \]
\[\text{ Now, } \]
\[ \text{ Work done by } \left( A + B + C \right) = \frac{4}{63}\]
\[\text{ Work done by } \left( B + C + D \right) = \frac{1}{14}\]
\[ \text{ Work done by } \left( C + D + A \right) = \frac{1}{18}\]
\[ \text{ Work done by } \left( D + A + B \right) = \frac{1}{21}\]
\[ \therefore \text{ Work done by working together } = \left( A + B + C \right) + \left( B + C + D \right) + \left( C + A + D \right) + \left( D + A + B \right)\]
\[ = \frac{4}{63} + \frac{1}{14} + \frac{1}{18} + \frac{1}{21}\]
\[ = \frac{4}{63} + \left( \frac{9 + 7 + 6}{126} \right) = \frac{4}{63} + \frac{22}{126}\]
\[ = \frac{4}{63} + \frac{11}{63} = \frac{15}{63}\]
\[ \therefore \text{ Work done by working together } = 3\left( A + B + C + D \right) = \frac{15}{63}\]
\[ \therefore \text{ Work done by } \left( A + B + C + D \right) = \frac{15}{63 \times 3} = \frac{5}{63}\]
\[ \text{ Thus, together they can do the work in } \frac{63}{5} \text{ days or } 12\frac{3}{5} \text{ days } .\]
APPEARS IN
संबंधित प्रश्न
Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on a road for 72 km. What would be her distance covered in the map?
A woker is paid Rs 200 for 8 days work. If he works for 20 days, how much will he get?
Expenditure of a family to number of members of the family are in direct proportion
If two quantities x and y vary directly with each other, then ______
If x and y are in direct proportion, then (x – 1) and (y – 1) are also in direct proportion.
When two quantities are related in such a manner that, if one increases, the other also increases, then they always vary directly.
Match each of the entries in Column I with the appropriate entry in Column II
| Column I | Column II |
| 1. x and y vary inversely to each other | A. `x/y` = Constant |
| 2. Mathematical representation of inverse variation of quantities p and q |
B. y will increase in proportion |
| 3. Mathematical representation of direct variation of quantities m and n |
C. xy = Constant |
| 4. When x = 5, y = 2.5 and when y = 5, x = 10 | D. `p oo 1/q` |
| 5. When x = 10, y = 5 and when x = 20, y = 2.5 | E. y will decrease in proportion |
| 6. x and y vary directly with each other | F. x and y are directly proportional |
| 7. If x and y vary inversely then on decreasing x | G. `m oo n` |
| 8. If x and y vary directly then on decreasing x | H. x and y vary inversely |
| I. `p oo q` | |
| J. `m oo 1/n` |
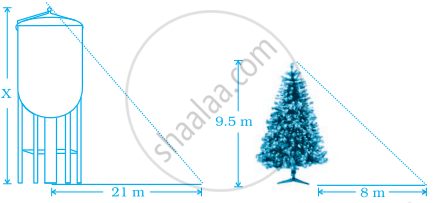
A water tank casts a shadow 21 m long. A tree of height 9.5 m casts a shadow 8 m long at the same time. The lengths of the shadows are directly proportional to their heights. Find the height of the tank.
The table shows the time four elevators take to travel various distances. Find which elevator is fastest and which is slowest.
| Distance (m) | Time (sec.) | |
| Elevator- A | 435 | 39 |
| Elevator- B | 448 | 28 |
| Elevator- C | 130 | 10 |
| Elevator- D | 85 | 5 |
How much distance will be travelled by elevators B and C separately in 140 sec? Who travelled more and by how much?
