Question

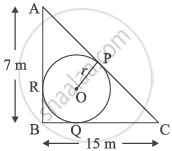
A backyard is in the shape of a triangle ABC with right angle at B. AB = 7m and BC = 15 m. A circular pit was dug inside it such that it touches the walls AC, BC and AB at P, Q and R respectively such that AP = x m.

Based on the above information, answer the following questions:

1. Find the length of AR in terms of x.   [1]
2. Write the type of quadrilateral BQOR.   [1]
3.   
   1. Find the length PC in terms of x and hence find the value of x.   [2]
                                             OR
   2. Find x and hence find the radius r of circle.   [2]

Answer 1

i. Given, AB = 7 m, BC = 15 m and AP = x m

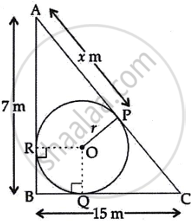
Hence, AP = AR     ...(Tangent drawn from an external point to the circle are equal in length)

∴ AR = x m

ii. Since AR = x m and AB = 7 m

∴ RB = (7 − x) m

Also, RB= BQ     ....(Tangents drawn from an external point to the circle)

OR = OQ     ...(radii of circle)

∠ORB = ∠OQB = 90°   ...(Angle between radius and tangent)

Also, ∠RBQ = 90°   ...(angle between the walls AB and BC)

Thus, ∠ROQ = 90°

Thus, `square`BQOR is square.

iii. 

a. Here, BC = 15 m

BQ = (7 − x) m

∴ QC = 15 − (7 − x)

or, QC = (8 + x) m

Also, QC = PC     ...(Tangents from an external point C to the circle)

i.e., PC = (8 + x) m

In right ΔABC, using Pythagoras theorem,

AC² = AB² + BC²

AC² = 7² + 15²

AC² = 49 + 225

 AC² = 274

⇒ AC = 16.55

⇒ AP + PC = 16.55

⇒ x + 8 + x = 16.55

⇒ 2x = 8.55

⇒ x = 4.275 ∼ 4.28 m

                                                       OR

b. From part (iii) (a), we get x = 4.28 m

From part (ii), we know that BQOR is a square

∴ BQ = OQ

⇒ r = 7 − x

⇒ r = 7 − 4.28

⇒ r = 2.72 m