Question

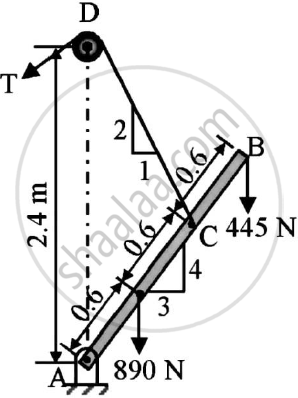
A boom AB is supported as shown in the figure by a cable runs from C over a small smooth pulley at D.
Compute the tension T in cable and reaction at A.Neglect the weight of the boom and size of the pulley.

Answer 1

Given : Beam AB is supported by a cable
To find : Tension T in cable
Reaction at A
Solution :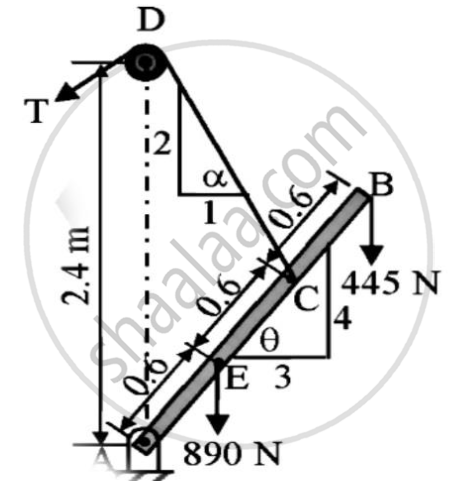

∠GCA = ∠BAF = θ
∠TCG = α
∠TCA = α + θ
= 63.4349o + 53.16°
= 116.5651°
∠TCB = 180o - 116.5651°
= 63.4349°
AC = AE+EC = 0.6 + 0.6 = 1.2
AB = AC + CB = 1.2 + 0.6 = 1.8
AF = ABcos θ = 1.8cos53.13 = 1.08
AH = AEcos θ = 0.6cos53.13 = 0.36
BEAM AB IS INDER EQUILIBRIUM
Applying conditions of equilibrium
Σ M_A = 0
-445 X AF – 890 X AH + Tsin63.4349 X AC = 0
T X 0.8944 X 1.2 = 445 X 1.08 + 890 X 0.36
T = 746.2877 N
Σ FX = 0
H_A - Tcos63.4349 = 0
H_A=333.75 N
Σ F_Y = 0
V_A + Tsin63.4349 – 890 – 445 = 0
V_A = 667.5 N
`R_A=sqrt(H_23^2+V_A^2)`

`R_A=sqrt((333.75)^2+(667.5)^2)`
`R_A=746.2877N`
Ф =`tan^-1((V_A)/H_A)`

Ф= `tan^-1((667.5)/333.75)`

Ф =63.4395°
Tension in cable = 746.2877 N (63.43949° in second quadrant)
Reaction at A = 746.2877 N (63.4395° in first quadrant)