Question

A capacitor of 150 pF is charged by a 200 V battery. The battery is then disconnected and the charge capacitor is connected to another uncharged capacitor of 50 pF. Calculate the difference between the final energy stored in the combined system and the initial energy stored in the single capacitor.

Answer 1

Given that,

V = 200 V

C = 150 pF

= 150 × 10⁻¹² F

`U_i =1/2CV^2`

`=1/2(150 xx 10^-12)(200)^2`

`=1/2 xx 15 xx 10^-11 xx 4 xx 10^4`

`=1/2 xx 60 xx 10^-7`

`=3 xx 10^-6 j`

Charge on capacitor C, given by

Q = CV = (150 × 10⁻¹²) (200)

= 30000 × 10⁻¹²

= 30 × 10⁻⁹c

= 30 nC

Now, charged capacitor is connected with the other capacitor C’ (= 50 pF). Then, charge on the capacitors is distributed.

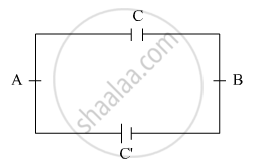
Suppose charge on C and C’ are q and q’ respectively.

According to charge conservation principle,

Q = q + q’ ……….. (1)

Also, Potential between the points A and B should be same.

`So, q/C = (q')/(C')`

`=> q/150 = (q')/(50`

`=> q/3 =q'`

`=> q =3q' .... (2)`

From equation (1) & (2)

`Q =3q' +q' = 4q'`

`=> q' = Q/4 = ((30nC)/4)`

`q' = 7.5nC`

`q = (3 xx 7.5) nC`

   `= 22.5nC`

`U_f = (q^2)/(2C)+(q'^2)/(2C')`

`=1/2 xx ((22.5 xx 10^-9)^2)/(150 xx 10^-12) + ((7.5 xx 10^-9)^2)/(2 xx 50 xx 10^-12)`

`= ((22.5 xx 22.5)/(2 xx 150)  + (7.5 xx 7.5)/(2 xx 50)) xx 10^-6`

`=(1.69 + 0.56) xx 10^-6`

`=2.25 xx 10^-6 j`

Difference of energy

`DeltaU =|U_f -U_f|`

         `=|2.25 xx 10^-6 - 3 xx 10^-6|`

`DeltaU =0.75 xx 10^-6 j`