Advertisements
Advertisements
प्रश्न
A charge is distributed uniformly over a ring of radius 'a'. Obtain an expression for the electric intensity E at a point on the axis of the ring. Hence, show that for points at large distance from the ring, it behaves like a point charge.
उत्तर
Here, we have a ring of radius a that carries a uniformly distributed positive total charge Q.
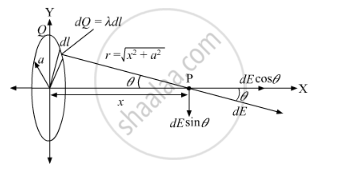
We have to calculate the electric field due to a ring at a point P lying a distance x from its centre along the central axis perpendicular to the plane of the ring.
As the charge is distributed uniformly over the ring, the charge density over the ring can be written as follows:
`lambda=Q/(2pia)`
Along the x-axis, the perpendicular components of the electric fields due to charge on the ring cancel each other out.
As there is same charge on both sides of the ring, the magnitude of the electric field at P due to the segment of charge dQ is given by
`dE=k_e (dQ)/r^2`
`E_x= int_"ring"k(dQ)/r^2costheta`
`=int_0^(2pia) k (lambdadl)/r^2 x/r`
`=klambda x/r^3 int_0^(2pia) dl`
`=klambda x/r^3 2pia`
`=kQ/(2pia)x/r^3 2pia`
`=KQx/r^3=KQ x/sqrt((x^2+a^2))^3`
1. At the centre of the ring, the electric field is zero as x = 0.
2. When x >> a , a can be neglected in the denominator compared to x, and the loop looks like a point charge at large distances.
`E=kQ x/sqrt((x^2+a^2)^3)`
`E=kQ/x^2, ("at "x" >> "a)`
संबंधित प्रश्न
What is the amount of work done in moving a point charge Q around a circular arc of radius ‘r’ at the centre of which another point charge ‘q’ is located?
Why must electrostatic field at the surface of a charged conductor be normal to the surface at every point? Give reason?
A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed ______.
A particle of charge q and mass m moves rectilinearly under the action of electric field E = A – Bx, where A and B are positive constants and x is distance from the point where particle was initially at rest then the distance traveled by the particle before coming to rest and acceleration of particle at that moment are respectively.
Let there be a spherically symmetric charge distribution with charge density varying as `rho("r") = rho_0(5/4 - "r"/"R")` upto r = R, and `rho("r") = 0` for r > R, where r is the distance from the origin. The electric field at a distance r(r < R) from the origin is given by _________.
Electric field at a point varies as r° for ______.
A charge of 4 × 10- 9c is distributed uniformly over the circumference of a conducting ring of radius 0.3 m. Calculate the field intensity at a point on the axis of the ring at 0.4 m from its center and also at the center?
Two equal point charges of the same sign are fixed on the y-axis, on either side of the origin equidistant from it, with the distance between them d. A third charge moves along the x-axis. The distance of the third charge from either of the two fixed charges when force on the third charge is maximum will be ______ cm.
[d = 10 cm]
An isolated point charge particle produces an electric field `vecE` at a point 3 m away from it. The distance of the point at which the field is `vecE/4` will be ______.
