Question

A circle with centre P is inscribed in the ABC. Side AB, side BC and side AC touch the circle at points L, M and N respectively.  Radius of the circle is r. 

Prove that: `"A" (triangle "ABC") =1/2 ("AB" + "BC" + "AC") xx "r"`

Answer 1

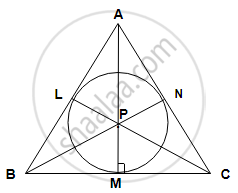
Given : P is the centre of the circle .

Construction : Join PL , PM , PN

Join APN ,BPN , CPL

To prove : `"A"(triangle"ABC") =1/2 ("AB" + "BC" + "AC") xx "r"`

Proof : 

PM ⊥ BC    

PN ⊥ AC

PL ⊥ AB 
....  `["AB , BC , AC are the tangent of the circle and distance between centre and tangent is always ⊥"]` 

and PM = PN = PL = r (radius)

Now , we can see that 

A(ΔABC) = [A(ΔAPB) + (ΔAPC) + (Δ BPC)]

`=1/2 "AB" xx"PL" + 1/2 "AC" xx "PN" + 1/2 "BC" xx "PM"`

`= 1/2 "AB" xx "r" + 1/2 "AC" xx "r" + 1/2 "BC" xx "r"`

`"A" (triangle "ABC") =1/2 ("AB" + "BC" + "AC") xx "r"`