Question

A complex number z is moving on `arg((z - 1)/(z + 1)) = π/2`. If the probability that `arg((z^3 -1)/(z^3 + 1)) = π/2` is `m/n`, where m, n ∈ prime, then (m + n) is equal to ______.

विकल्प

• 2.00

• 3.00

• 4.00

• 5.00

Answer 1

A complex number z is moving on `arg((z - 1)/(z + 1)) = π/2`. If the probability that `arg((z^3 -1)/(z^3 + 1)) = π/2` is `m/n`, where m, n ∈ prime, then (m + n) is equal to 5.00.

Explanation:

`arg((z - 1)/(z + 1)) = π/2`

i.e. z is moving on a semicircle as shown

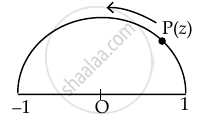
If `arg((z^3 - 1)/(z^3 + 1)) = π/2`

⇒ z³ = e^iθ, 0 < θ < π

⇒ z = `e^(i((θ + 2kπ)/3)`, k = –1, 0, 1

⇒ z = `e^((iθ)/3), e^(i((θ + 2π)/3)), e^(i((θ - 2π)/3)`, 0 < θ < π

Whose locus is shown below

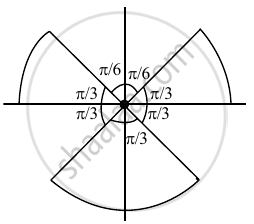
∴ Locus of z is the union of 3 are as shown above

⇒ Probability = `2/3`

⇒ m + n = 5