Advertisements
Advertisements
प्रश्न
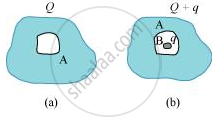
(a) A conductor A with a cavity as shown in Fig (a) is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor.
(b) Another conductor B with charge q is inserted into the cavity keeping B insulated from A. Show that the total charge on the outside surface of A is Q + q [Fig. (b)].
(c) A sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way.
उत्तर
(a) Let us consider a Gaussian surface that is lying wholly within a conductor and enclosing the cavity. The electric field intensity E inside the charged conductor is zero.
Let q is the charge inside the conductor and `in_0` is the permittivity of free space.
According to Gauss’s law,
Flux, `phi = vec"E".vec("ds") = "q"/in_0`
Here, E = 0
`"q"/in_0 = 0`
∵ ∈0 `≠` 0
∴ q = 0
Therefore, charge inside the conductor is zero.
The entire charge Q appears on the outer surface of the conductor.
(b) The outer surface of conductor A has a charge of amount Q. Another conductor B having charge +q is kept inside conductor A and it is insulated from A. Hence, a charge of amount −q will be induced in the inner surface of conductor A and +q is induced on the outer surface of conductor A. Therefore, the total charge on the outer surface of conductor A is Q + q.
(c) A sensitive instrument can be shielded from the strong electrostatic field in its environment by enclosing it fully inside a metallic surface. A closed metallic body acts as an electrostatic shield.
APPEARS IN
संबंधित प्रश्न
A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is `(sigma/(2in_0)) hat"n"`. where `hat"n"` is the unit vector in the outward normal direction, and `sigma` is the surface charge density near the hole.
The number of electrons in an insulator is of the same order as the number of electrons in a conductor. What is then the basic difference between a conductor and an insulator ?
Answer the following question.
State the units of linear charge density.
Two charges 5 μC and -4μC are kept 5.0 m apart at points A and B respectively. How much work will have to be done to move the charge at A through a distance of 5.0 m further away from point B along the line BA?
Infinite charges of magnitude q each are lying at x = 1, 2, 4, 8 ... metre on X-axis. The value of the intensity of the electric field at point x = 0 due to these charges will be ______
In a region where intensity of electric field is 5 NC-1, 40 lines of electric force are crossing per square metre. The number of lines crossing per square metre where intensity of electric field is 10 NC-1 will be ______
Which of the following is three-dimensional continuous charge distribution?
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.7 × 10–22 C/m2. What is electric field intensity E:
- in the outer region of the first plate, and
- between the plates?
There is a uniform spherically symmetric surface charge density at a distance Ro from the origin. The charge distribution is initially at rest and starts expanding because of mutual repulsion. The figure that represents best the speed V (R(t)) of the distribution as a function of its instantaneous radius R(t) is:
An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
