Advertisements
Advertisements
प्रश्न
A convex lens of focal length 25 cm is placed coaxially in contact with a concave lens of focal length 20 cm. Determine the power of the combination. Will the system be converging or diverging in nature?
उत्तर
We have focal length of convex lens,
`f_1 = +25 cm = +0.25 m`and focal lenghth of conceave
lens, f2 =-20 cm =-0.20 m
Equivalent focal length, `f= 1/f_1 +1/f_2 =1/25 +1/-20=-1/100`
∴ F =- 100 cm
Power of convex lens, `P_1 = 1/f_1 = 1/0.25`
Power of convex lens,`P_2 = 1/f_2 = 1/- 0.20`
Power of the combination,
`P = P_1+P_2 = 1/0.25 + 1/-0.20 = 100/25 +100/-20 = (400 - 500)/100 = (-100)/100 = -1D`
The focal length of the combination =–1 m = –100 cm.
As the focal length is in negative, the system will be diverging in nature.
APPEARS IN
संबंधित प्रश्न
A mobile phone lies along the principal axis of a concave mirror. Show, with the help of a suitable diagram, the formation of its image. Explain why magnification is not uniform.
Obtain the mirror formula and write the expression for the linear magnification.
A convex lens of focal length 30 cm is placed coaxially in contact with a concave lens of focal length 40 cm. Determine the power of the combination. Will the system be converging or diverging in nature?
An object AB is kept in front of a concave mirror as shown in the figure.
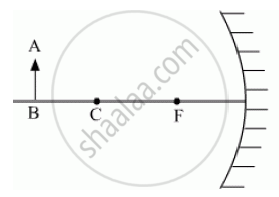
(i) Complete the ray diagram showing the image formation of the object.
(ii) How will the position and intensity of the image be affected if the lower half of the mirror’s reflecting surface is painted black?
Use Huygens’ geometrical construction to show the behavior of a plane wavefront.
(i) Passing through a biconvex lens;
(ii) Reflecting by a concave mirror
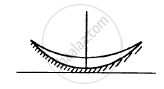
A concave mirror of radius R is kept on a horizontal table (See figure). Water (refractive index = μ) is poured into it up to a height h. Where should an object be placed so that its image is formed on itself?

The convex surface of a thin concavo-convex lens of glass of refractive index 1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface as shown in figure. (a) Where should a pin be placed on the axis so that its image is formed at the same place? (b) If the concave part is filled with water (μ = 4/3), find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.
A particle is moving at a constant speed V from a large distance towards a concave mirror of radius R along its principal axis. Find the speed of the image formed by the mirror as a function of the distance x of the particle from the mirror.
A small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time t < d/V, (b) at a time t > d/V.
In the case of a concave mirror of focal length f , when an object is kept between f and 2 f , show that its image is formed beyond 2 f .
