Advertisements
Advertisements
प्रश्न
A copper sphere of radius 3cm is melted and recast into a right circular cone of height 3cm.find radius of base of cone?
उत्तर
Given radius of sphere = 3cm
Volume of a sphere =`4/3pir^3`
`=4/3xxpixx3^3cm^3` .........(1)
Given sphere is melted and recast into a right circular cone
Given height of circular cone = 3cm.
Volume of right circular cone `=pir^2xx1/3`
`=pi/3(r)^2xx3cm^2` ..........(2)
Equating 1 and 2 we get
`4/3pixx3^3=1/3pi(r)^2xx3`
`r^2=(4/3pixx3^3)/pi`
r2 = 36cm
r = 6cm
∴ Radius of base of cone(r) = 6cm
APPEARS IN
संबंधित प्रश्न
A well of diameter 2m is dug14m deep. The earth taken out of it is spread evenly all around it to form an embankment of height 40cm. Find width of the embankment?
A hollow sphere of internal and external radii 2cm and 4cm is melted into a cone of basse radius 4cm. find the height and slant height of the cone______?
A solid metallic cuboid of dimensions 9 m × 8 m × 2 m is melted and recast into solid cubes of edge 2 m. Find the number of cubes so formed.
A solid right circular cone of height 60 cm and radius 30 cm is dropped in a right circular cylinder full of water, of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres.
A solid metallic sphere of radius 8 cm is melted and recast into spherical balls each of radius 2 cm. Find the number of spherical balls obtained.
A copper sphere of diameter 18 cm is drawn into a wire of diameter 4 mm. Find the length of the wire.
A metallic cylinder of radius 8 cm and height 2 cm is melted and converted into a right circular cone of height 6 cm. The radius of the base of this cone is
The boundary of the shaded region in the given diagram consists of three semicircular areas, the smaller ones being equal and it’s diameter 5 cm, if the diameter of the larger one is 10 cm,
calculate:
(i) The length of the boundary,
(ii) The area of the shaded region. (Take π = 3.14)

The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
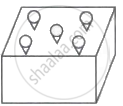
Read the following passage and answer the questions given below.
|
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.