Advertisements
Advertisements
प्रश्न
A cylinder rolls on a horizontal place surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
उत्तर
Let vc be the translational velocity of the cylinder.
Let ω be the rotational velocity of the cylinder.
Let r be the radius of the cylinder.
For rolling, we have
vc = rω
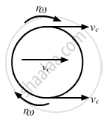
Speed of the highest point = vc + rω = 2vc
\[\Rightarrow2 \times 25\text{ m/s}=50\text{ m/s}\]
APPEARS IN
संबंधित प्रश्न
Derive an expression for kinetic energy, when a rigid body is rolling on a horizontal surface without slipping. Hence find kinetic energy for a solid sphere.
Read each statement below carefully, and state, with reasons, if it is true or false;
For perfect rolling motion, work done against friction is zero.
A stone of mass 2 kg is whirled in a horizontal circle attached at the end of 1.5m long string. If the string makes an angle of 30° with vertical, compute its period. (g = 9.8 m/s2)
Can an object be in pure translation as well as in pure rotation?
A sphere cannot roll on
A hollow sphere is released from the top of an inclined plane of inclination θ. (a) What should be the minimum coefficient of friction between the sphere and the plane to prevent sliding? (b) Find the kinetic energy of the ball as it moves down a length l on the incline if the friction coefficient is half the value calculated in part (a).
Answer in Brief:
A rigid object is rolling down an inclined plane derive the expression for the acceleration along the track and the speed after falling through a certain vertical distance.
A pendulum consisting of a massless string of length 20 cm and a tiny bob of mass 100 g is set up as a conical pendulum. Its bob now performs 75 rpm. Calculate kinetic energy and increase in the gravitational potential energy of the bob. (Use π2 = 10)
The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is, ______
What is the condition for pure rolling?
What is the difference between sliding and slipping?
Discuss rolling on an inclined plane and arrive at the expression for acceleration.
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with velocity of 10 emfs. The total kinetic energy of sphere is ______.
A man is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre at an angular velocity `omega`. The tension in the strings is F. If the length of string and angular velocity are doubled, the tension in string is now ____________.
The power (P) is supplied to rotating body having moment of inertia 'I' and angular acceleration 'α'. Its instantaneous angular velocity is ______.
A 1000 kg car has four 10 kg wheels. When the car is moving, fraction of total K.E. of the car due to rotation of the wheels about their axles is nearly (Assume wheels be uniform disc)
A circular disc reaches from top to bottom of an inclined plane of length 'L'. When it slips down the plane, it takes time ' t1'. when it rolls down the plane, it takes time t2. The value of `t_2/t_1` is `sqrt(3/x)`. The value of x will be ______.
The least coefficient of friction for an inclined plane inclined at angle α with horizontal in order that a solid cylinder will roll down without slipping is ______.
