Question

A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure. The radius of vessel is 5 cm and the angular speed of rotation is ω rad s^-1. The difference in the height, h (in cm) of liquid at the centre of vessel and at the side will be :

विकल्प

• `(5omega^2)/(2"g")`

• `(2omega^2)/(25"g")`

• `(25omega^2)/(2"g")`

• `(2omega^2)/(5"g")`

Answer 1

`bb((25omega^2)/(2"g"))`

Explanation:

Given: Radius of a cylindrical vessel is R = 5 cm, the angular speed of the vessel is ω rad/s.

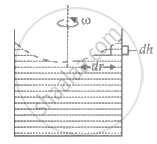To find: h, the difference in height of the liquid at the periphery of the vessel and at the centre.

Let ρ be the density of the liquid.

Balancing the pressure on the liquid column due to weight and due to rotational motion:

(ρω²r)dr = ρgdh

`int_0^"R"(omega^2r)"dr" = "g"int_0^"h""dh"`

h = `(omega^2"R"^2)/(2"g")`

= `(25omega^2)/(2"g")`