Advertisements
Advertisements
प्रश्न
Derive the formula : v = u + at, where the symbols have usual meanings.
उत्तर
Consider a body has initial velocity (u) . Suppose it is subjected to a uniform acceleration (a) such that after time (t) its final velocity becomes (v). Now, from the definition of acceleration we know that:
Acceleration = `"Change in velocity"/"Time taken"`
The above expression can also be written as ,
`a = (v-u)/t`
On further simplification, we get the 1st equation of motion,
v = u + at
Where,
(a) - Acceleration
(v) - Final velocity
(u) - Initial velocity
(t) - Time taken
The equation v = u + at is called the first equation of motion and is used to calculate the velocity 'v' acquired by a body in time 't'.
APPEARS IN
संबंधित प्रश्न
Give one example of a situation in which a body has a certain average speed but its average velocity is zero.
Fill in the following blank with a suitable word:
Acceleration is the rate of change of ______ It is measured in ______
A boy is sitting on a merry-go-round which is moving with a constant speed of 10 m s−1. This means that the boy is :
Differentiate between uniform acceleration and variable acceleration.
What do you understand by the term acceleration?
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
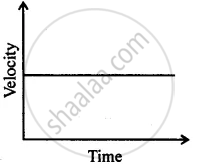
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
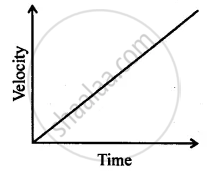
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
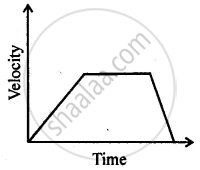
An electron moving with a velocity of 5 × 104 ms−1 enters into a uniform electric field and acquires a uniform acceleration of 104 ms–2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover at this time?
Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the heights reached by them would be in the ratio of `"u"_1^2 : "u"_2^2` (Assume upward acceleration is –g and downward acceleration to be +g)
