Question

A man is moving away from a tower 41.6 m high at a rate of 2 m/s. If the eye level of the man is 1.6 m above the ground, then the rate at which the angle of elevation of the top of the tower changes, when he is at a distance of 30 m from the foot of the tower, is

विकल्प

• `- 4/125` rad/s

• `- 2/25` rad/s

• `- 1/625` rad/s

• None of these

Answer 1

`- 4/125` rad/s

Explanation:

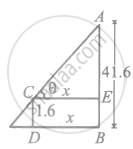
Let CD be the position of man at any time t.

Let BD be x.

Then EC = x.

Let ∠ACE be θ.

Given AB = 41.6 cm, CD = 1.6 m and `(dx)/(dt)` = 2 m/s.

AE = AB – EB = AB – CD = 41.6 – 1.6 = 40 m

We have to find `(d theta)/(dt)` when x = 30 m.

From ΔAEC, tan θ = `(AE)/(EC) = 40/x`

Differentiating w.r.t. to t, sec²θ `(d theta)/(dt) = (-40)/x^2 (dx)/(dt)`

or sec²θ `(d theta)/(dt) = (- 40)/x^2 xx 2`

or `(d theta)/(dt) = (- 80)/x^2 cos^2 theta = - 80/x^2 x^2/(x^2 + 40^2) = - 80/(x^2 + 40^2)`.

When x = 30 m, `(d theta)/(dt) = - 80/(30^2 + 40^2) = - 4/125` rad/s.