Question

A person standing on the bank of a river observes that the angle of elevation of the top of a tower on the opposite bank is 60°. When he moves 30 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tower and width of the river. (Take `sqrt3` = 1.732) 

Answer 1

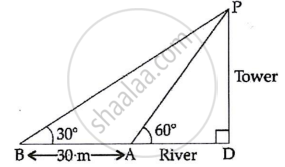
Let the height of the tower (PD) be h m and width of the river (AD) be x m 

In ΔAOD, 

tan A = `(PD)/(AD)` 

tan 60° = `h/x`

`sqrt3 = h/x`

h = `xsqrt3`            ...(i)

In ΔDBP, 

tan B = `(PD)/(DB)`

tan B = `h/(x + 30)`

`1/sqrt3 = h/(x + 30)`

x + 30 = `sqrt3h`

x + 30 = 3x

x = 15 m

∴ width of the river 15 m

h = x`sqrt3`     ....from (i)

= 15 × 1.732

= 25.980 m

∴ Height of the tower is 25.98 m