Advertisements
Advertisements
प्रश्न
A rectangular hall is 12 m long and 6 m broad. Its flooring is to be made of square tiles of side 30 cm. How many tiles will fit in the entire hall? How many would be required if tiles of side 15 cm were used?
उत्तर
Hall length = 12 m = 12 × 100 = 1200 cm
Hall breadth = 6 m = 6 × 100 = 600 cm
∴ Hall area = length × breadth
= 1200 × 600
∴ Hall area = 720000 cm2
Now,
Area of tile (side 30 cm) = (side)2
= (30 cm)2
= 900 cm2
∴ Total no. of tiles required = `"Hall area"/"Area of tile"`
= `720000/900`
= 800 tiles
Now,
If the side of the tile is 15 cm then its area = (15)2
= 225 cm2
∴ Total no. of tiles required = `720000/225`
= 3200 tiles
Hence,
When the side is 30 cm, then tiles = 800 tiles,
and side 15 cm the tiles = 3200 tiles.
संबंधित प्रश्न
If the side of a square is 12 cm, find its area.
Find the area of the following rectangle
length = 9 m and breadth = 6 m
The side of a square is 6 cm. The length of a rectangle is 10 cm and its breadth is 4 cm. Find the perimeter and area of both the square and rectangle
Here is a rectangle of an area of 20 square cm.

Draw one straight line in this rectangle to divide it into two equal rectangles. What is the area of each of the smaller rectangles?
If length of a rectangle is halved and breadth is doubled then the area of the rectangle obtained remains same.
The length and breadth of the three rectangles are as given below:
- 9 m and 6 m
- 17 m and 3 m
- 4 m and 14 m
Which one has the largest area and which one has the smallest?
The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m.?
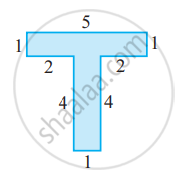
Split the following shape into rectangle and find their area. (The measures are given in centimetres).
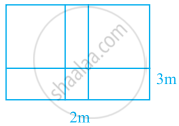
A school playground is divided by a 2 m wide path which is parallel to the width of the playground, and a 3 m wide path which is parallel to the length of the ground in the given figure. If the length and width of the playground are 120 m and 80 m respectively, find the area of the remaining playground.