Question

A solid disc and a ring, both of radius 10 cm are placed on a horizontal table simultaneously, with initial angular speed equal to 10 π rad s^-1. Which of the two will start to roll earlier? The coefficient of kinetic friction is μ_k = 0.2.

Answer 1

Disc Radii of the ring and the disc, r = 10 cm = 0.1 m

Initial angular speed, ω₀ =10 π rad s^–1

Coefficient of kinetic friction, μ_k = 0.2

Initial velocity of both the objects, u = 0

Motion of the two objects is caused by frictional force. As per Newton’s second law of motion, we have frictional force, f = ma

μ_kmg= ma

Where,

a = Acceleration produced in the objects

m = Mass

∴a = μ_kg … (i)

As per the first equation of motion, the final velocity of the objects can be obtained as:

v = u + at

= 0 + μ_kgt

= μ_kgt … (ii)

The torque applied by the frictional force will act in perpendicularly outward direction and cause the reduction in the initial angular speed.

Torque, τ= –Iα

α = Angular acceleration

μ_xmgr = –Iα

`:.alpha = (-mu_kmgr)/I` ....(iii)

 Using the first equation of rotational motion to obtain the final angular speed:

`omega = omega_0 + alphat`

`= omega_0 + (-mu_kmgr)/It`  ....(iv)

Rolling starts when linear velocity, v = rω

`:.v= r(omega_0 - (mu_kgmrt)/I)` ...(v)

Equating equations (ii) and (v), we get:

`mu_kgt = r (omega_0 - (mu_kgmrt)/I)`

`= romega_0 - (mu_kgmr^2t)/I`   .....(vi)

For the ring: `I =mr^2`

`:. mu"gt" = romega_0 - (mu_kgmr^2t)/(mr^2)`

`= romega_0 -mu_kgmt_r`

`2mu_k"gt" = romega_0`

`:. t_r = (rw_0)/(2mu_kg)`

`= (0.1xx10xx3.14)/(2xx0.2xx9.8) = 0.80s` .....(vii)

For the disc: `I = 1/2mr^2`

`:.mu_k"gt"_d = rw_0 (mukgmr^2t)/(1/2mr^2)`

`= romega_0 - 2mu_k"gt"`

`3mu_k"gt"_d = romega_0`

`:.t_d = (romega_0)/(3mu_kg)`

`= (0.1xx10xx3.14)/(3xx0.2xx9.8) = 0.53 s`  ...(viii)

Since `t_d > t_r` the disc will start rolling before the ring.

 

Answer 2

When a disc or ring starts rotatory motion on a horizontal surface, an initial translational velocity of the centre of mass is zero.

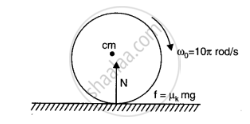
The frictional force causes the centre of mass to accelerate linearly but frictional torque causes angular retardation. As force of normal reaction N = mg, hence frictional force f = u_k N = u_k mg.
For linear motion f = u_k . mg = ma ———-(i)

and for rotational motion `t = f.R = mu_k mg.R = -ialpha` ....(ii)

Let perfect rolling motion starts at time t, when `v =  Romega`

From (i) `a =  mu_k.g`

`v = u + at = 0 + mu_k.g.t`

From (ii) `alpha  = - (mu_k.mgR)/I = -( mu_k.mgR)/(mK^2) = - (mu_k.gR)/K^2`  ....(iii)

`:. omega = omega_0 + alphat = omega_0 - (mu_k.gR)/K^2 t`  ...(iv)

Since `v  =  Romega =, "hence " mu_k.g.t = R[omega_0 - mu_k. (gR)/K^2t]`

`=> t^2 = (Romega_0)/(mu_k .g(1+R^2/K^2))`

For disc `K^2 =  R^2/2, "hence " t = (omega_0R)/(mu_k.g(1+R^2/(R^2"/"2))) = (omega_0R)/(3mu_k.g)`

For ring `K^2 = R^2` hence  `t = (mu_0R) /(mu_k.g(1+R^2/R^2)) = (omega_0R)/(2mu_k.g)`

Thus it is clear that disc will start to roll earlier. The actual time at which disc start rolling will be

`t = (omega_0R)/(2mu_k.g) = ((10pi)xx(0.1))/(3xx(0.2)xx9.8) = 0.538`