Advertisements
Advertisements
प्रश्न
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone.
उत्तर
(i) Whenever we placed a solid right circular cone in a right circular cylinder with full of water,
Then volume of a solid right circular cone is equal to the volume of water failed from the cylinder.
(ii) Total volume of water in a cylinder is equal to the volume of the cylinder.
(iii) Volume of water left in the cylinder = Volume of the right circular cylinder – volume of a right circular cone.
Now, given that
Height of a right circular cone = 120 cm
Radius of a right circular cone = 60 cm
∴ Volume of a right circular cone
= `1/3 pir^2 xx h`
= `1/3 xx 22/7 xx 60 xx 60 xx 120`
= `22/7 xx 20 xx 60 xx 120`
= 144000π cm3
∴ Volume of a right circular cone
= Volume of water falled from the cylinder
= 144000π cm3 ...[From point (i)]
Given that, height of a right circular cylinder = 180 cm
And radius of a right circular cylinder
= Radius of a right circular cone
= 60 cm
∴ Volume of a right circular cylinder
= πr2 × h
= π × 60 × 60 × 180
= 648000π cm3
So, volume of a right circular cylinder
= Total volume of water in a cylinder
= 648000π cm3 ...[From point (ii)]
From point (iii),
Volume of water left in the cylinder
= Total volume of water in a cylinder – Volume of water falled from the cylinder when sold cone is placed in it
= 648000π – 144000π
= 504000π
= `504000 xx 22/7`
= 1584000 cm3
= `1584000/(10)^6 m^3`
= 1.584 m3
Hence, the required volume of water left in the cylinder is 1.584 m3.
APPEARS IN
संबंधित प्रश्न
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
A copper rod of diameter 2 cm and length 10 cm is drawn into a wire of uniform thickness and length 10 m. Find the thickness of the wire.
The volume of a right circular cylinder with its height equal to the radius is `25"1"/7` cm3. Find the height of the cylinder.
A cubical ice-cream brick of edge 22 cm is to be distributed among some children by filling ice-cream cones of radius 2 cm and height 7 cm up to the brim. How many children will get the ice-cream cones?
A hollow metallic sphere with external diameter 8 cm and internal diameter 4 cm is melted and moulded into a cone of base radius 8 cm. The height of the cone is
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
The boundary of the shaded region in the given diagram consists of three semicircular areas, the smaller ones being equal and it’s diameter 5 cm, if the diameter of the larger one is 10 cm,
calculate:
(i) The length of the boundary,
(ii) The area of the shaded region. (Take π = 3.14)

A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of entire capsule is 2 cm. The capacity of the capsule is ______.
Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Read the following passage and answer the questions given below.
|
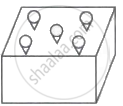
A solid cuboidal toy is made of wood. It has five cone-shaped cavities to hold toy carrots. The dimensions of the toy cuboid are – 10 cm × 10 cm × 8 cm. Each cone carved out – Radius = 2.1 cm and Height = 6 cm
|
- Find the volume of wood carved out to make five conical cavities.
- Find the volume of the wood in the final product.