Question

A sphere of mass 'm' moving with velocity 'v' collides head-on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is ______. ( e is coefficient of restitution and collision is inelastic)

विकल्प

• `("e"-1)/2`

• `"e"/2`

• `("e"+1)/2`

• e

Answer 1

A sphere of mass 'm' moving with velocity 'v' collides head-on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is `underlinebb(("e"+1)/2)`. ( e is coefficient of restitution and collision is inelastic)

Explanation:

Before collision              After collision

 

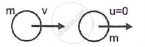
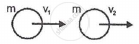
mV + 0 = mV₁ + mV₂

V₁ + V₂ = V

e = `("V"_2-"V"_1)/("u"_1-"u"_2)`

e = `("V"_2-"V"_1)/("V"_1-0)`

Coefficient of restitution, e

eV = V₂ - V₁

eV + V = 2V₂

⇒ V₂ = `("V"("e"+1))/2`

∴ Ratio, `"V"_2/"V"=("e"+1)/2`