Advertisements
Advertisements
प्रश्न
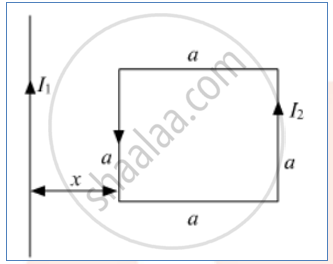
A square loop of side 'a' carrying a current I2 is kept at distance x from an infinitely long straight wire carrying a current I1 as shown in the figure. Obtain the expression for the resultant force acting on the loop.
उत्तर
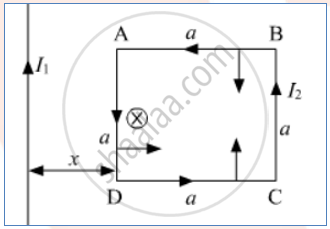
According to the right-hand screw rule, the magnetic field will be into the plane across the loop Force on length AD
F = Bil
`F_1 = (mu_0I_1I_2a)/(2pix)`
Force on length BC
F = Bil
`F_2 = (mu_0I_1I_2a)/(2pi(x + a))`
Force on AB and CD will be equal and opposite . Hence, they'll cancel out. Force on the loop
`F_"Net" = F_1 - F_2`
= `(mu_0I_1I_2a)/(2pi)[1/x - 1/((x + a))]`
`F_("Net") = (mu_0I_1I_2a)/(2pi)[(x + a - x)/((x + a)x)] = (mu_0I_1I_2a^2)/(2pi(x + a)x)`
`F_("Net") = (mu_0I_1I_2a^2)/(2pix(x + a))` (Towards left)
APPEARS IN
संबंधित प्रश्न
A square coil of side 10 cm consists of 20 turns and carries a current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30° with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil?
A rectangular loop of wire of size 4 cm × 10 cm carries a steady current of 2 A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
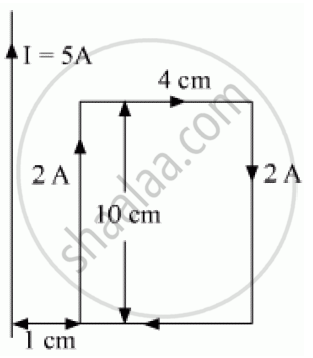
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.
A magnetised needle of magnetic moment 4.8 × 10−2 JT−1 is placed at 30° with the direction of uniform magnetic field of magnitude 3 × 10−2 T. Calculate the torque acting on the needle.
The rectangular wire-frame, shown in figure, has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t = 0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. Find this velocity v0. (c) Show that the velocity at time t is given by
v = v0(1 − e−Ft/mv0).
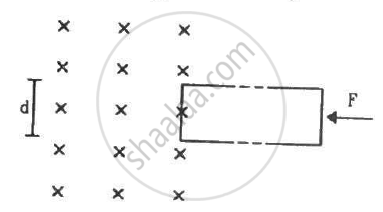
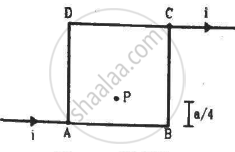
Figure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
Find the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
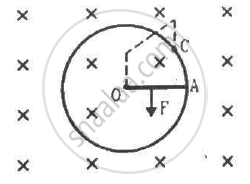
Figure shows a conducting circular loop of radius a placed in a uniform, perpendicular magnetic field B. A thick metal rod OA is pivoted at the centre O. The other end of the rod touches the loop at A. The centre O and a fixed point C on the loop are connected by a wire OC of resistance R. A force is applied at the middle point of the rod OAperpendicularly, so that the rod rotates clockwise at a uniform angular velocity ω. Find the force.
A planar loop of rectangular shape is moved within the region of a uniform magnetic field acting perpendicular to its plane. What is the direction and magnitude of the current induced in it?
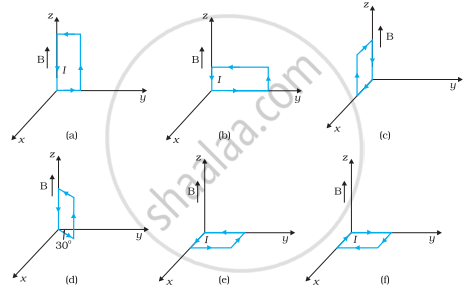
A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in fig.? What is the force on each case? Which case corresponds to stable equilibrium?
- Assertion (A): The deflecting torque acting on a current-carrying loop is zero when its plane is perpendicular to the direction of the magnetic field.
- Reason (R): The deflecting torque acting on a loop of the magnetic moment `vecm` in a magnetic field `vecB` is given by the dot product of `vecm` and `vecB`.
