Advertisements
Advertisements
प्रश्न
A square plate of side 'x' cm is 4 mm thick. If its volume is 1440 cm3; find the value of 'x'.
उत्तर
Volume of the square plate = Volume of a cuboid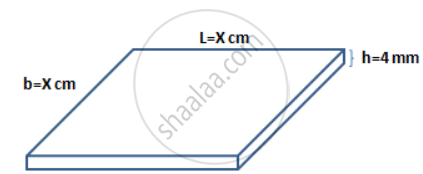
h = 4mm
= `(4)/(10)"cm"`
= 0.4cm
Volume of the square plate
= l x b x h
1440 = X x X x 0.4
1440 = x2 x 0.4
x2 = `(1440)/(0.4)` = 3600
x = `sqrt(3600)`
∴ x = 60cm.
APPEARS IN
संबंधित प्रश्न
The paint in a certain container is sufficient to paint on area equal to 9.375 m2. How manybricks of dimension 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
On a particular day, the rain fall recorded in a terrace 6 m long and 5 m broad is 15 cm. The quantity of water collected in the terrace is
If each edge of a cube is increased by 50%, the percentage increase in its surface area is
If l is the length of a diagonal of a cube of volume V, then
A tank 30 m long, 24 m wide, and 4.5 m deep is to be made. It is open from the top. Find the cost of iron-sheet required, at the rate of ₹ 65 per m2, to make the tank.
The height of a rectangular solid is 5 times its width and its length is 8 times its height. If the volume of the wall is 102.4 cm3, find its length.
The height of a circular cylinder is 20 cm and the diameter of its base is 14 cm. Find:
(i) the volume
(ii) the total surface area.
An open box of length 1.5 m, breadth 1 m, and height 1 m is to be made for use on a trolley for carrying garden waste. How much sheet metal will be required to make this box? The inside and outside surface of the box is to be painted with rust-proof paint. At a rate of 150 rupees per sqm, how much will it cost to paint the box?
A room is 5m long, 2m broad and 4m high. Calculate the number of persons it can accommodate if each person needs 0.16m3 of air.
The surface area of a cuboid formed by joining face to face 3 cubes of side x is 3 times the surface area of a cube of side x.
