Advertisements
Advertisements
प्रश्न
A stone of 1 kg is thrown with a velocity of 20 m s−1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
उत्तर
Mass of the stone (m) = 1kg
Distance travelled (s) = 50 m
Initial velocity of the stone (u) = 20 m/s
The final velocity of the stone (v) = 0 m/s
From the third equation of motion
v2 - u2 = 2as
02 - (20)2 = 2 × a × 50
02 - (20)2 = 100a
a = `(-400)/100`
a = -4 m s-2
The frictional force between the stone and ice
F = m × a
F = 1 × -4
= -4 N
Therefore, the frictional force between the stone and ice = -4 N
APPEARS IN
संबंधित प्रश्न
If action is always equal to the reaction, explain how a horse can pull a cart.
Using a horizontal force of 200 N, we intend to move a wooden cabinet across a floor at a constant velocity. What is the friction force that will be exerted on the cabinet?
What is the force which produces an acceleration of 1 m /s2 in a body of mass 1 kg ?
A girl weighing 25 kg stands on the tloor. She exerts a downward force of 250 N on the floor. What force does the floor exert on her ?
Why does a gunman get a jerk on firing a bullet ?
Explain how a rocket works.
If a man jumps out from a boat, the boat moves backwards. Why ?
Name the law involved in the following situation :
when person A standing on roller skates pushes another person B (also standing on roller skates) and makes him move to the right side, then the person A himself gets moved to the left side by an equal distance.
According to the third law of motion, action and reaction :
Consider a frame that is made up of two thin massless rods AB and AC as shown in the figure. A vertical force `vec"P"` of magnitude 100 N is applied at point A of the frame.
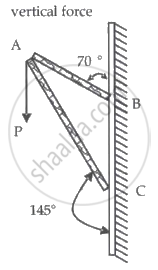
Suppose the force is `vec"P"` resolved parallel to the arms AB and AC of the frame.
The magnitude of the resolved component along the arm AC is xN.
The value of x, to the nearest integer, is ______.
[Given: sin(35°) = 0.573, cos(35°) = 0.819, sin(110°) = 0.939, cos(110°) = –0.342]
