Question

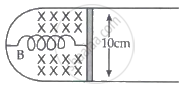
A thin strip 10 cm long is on a U-shaped wire of negligible resistance and it is connected to a spring of spring constant 0.5 Nm^-1. The assembly is kept in a uniform magnetic field of 0.1 T. If the strip is pulled from its equilibrium position and released, the number of oscillations it performs before its amplitude decreases by a factor of e is N. If the mass of the strip is 50 grams, its resistance is 10 Ω, and air drag is negligible, N will be close to ______.

विकल्प

• 1000

• 50000

• 5000

• 10000

Answer 1

A thin strip 10 cm long is on a U-shaped wire of negligible resistance and it is connected to a spring of spring constant 0.5 Nm^-1 (see figure). The assembly is kept in a uniform magnetic field of 0.1 T. If the strip is pulled from its equilibrium position and released, the number of oscillations it performs before its amplitude decreases by a factor of e is N. If the mass of the strip is 50 grams, its resistance is 10 Ω, and air drag is negligible, N will be close to 5000.

Explanation:

Given: Length of the strip is l = 10 cm, the resistance of the U-shaped wire is negligible, the spring constant of the spring connected to the strip is k = 0.5 N/m, the magnitude of the applied magnetic field is B = 0.1 T, the mass of strip is m = 50 g, the resistance of strip is R = 10 Ω, When pulled from its equilibrium position and released, the number of oscillations performed by the strip before its amplitude decreases by a factor of e is N.

To find: N's value.

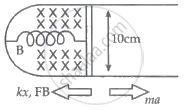
When the strip is pulled out of its equilibrium position, two forces act on it to try to return it to its equilibrium position, as shown in the diagram above.

So, -kx - F_B = ma ....(F_B = -Bil, is the magnetic field's force.)

-kx - Bil = ma

[`i = (Blv)/R` denotes the current flowing through the strip, and v denotes its velocity.]

`-kx - (B^2l^2v)/R = ma`

Put ν = `(dx)/(dt), a = (d^2x)/(dt^2)` in the equation above.

`-kx - (B^2l^2)/R(dx/dt) = m((d^2x)/(dt^2))`

`m((d^2x)/(dt^2)) + (B^2l^2)/(R)((dx)/(dt)) + kx = 0`

The equation for a damped simple harmonic motion given above has the following amplitude:

A(t) = A₀ exp`((B^2l^2)/(2Rm)t)`

Put A(t) = `A_0/e` in the above equation.

`A_0/e = A_0 exp(-(B^2l^2)/(2Rm)t)`

`(B^2l^2)/(2Rm)t = 1`

`t = (2Rm)/(B^2l^2)`

Insert the values here:

`t = (2 xx 10 xx 50 xx 10^-3)/((0.1)^2 xx (10 xx 10^-2)^2) = 10000 s`

The spring's oscillation period is:

`T = 2pisqrt(m/k) = 2pisqrt((50 xx 10^-3)/0.5)` = 2s

The total amount of oscillations in time t is thus:

`N = t/T = 10000/2 = 5000`