Question

A uniform cylinder of mass M and radius R is to be pulled over a step of height a (a < R) by applying a force F at its centre 'O' perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of F required is:

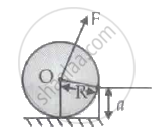
विकल्प

• `"Mg"sqrt(1-(("R"-"a")/"R")^2)`

• `"Mg"sqrt(1-"a"^2/"R"^2)`

• `"Mg"sqrt("R"/("R"-"a")-1`

• Mg `"a"/"R"`

Answer 1

`bb("Mg"sqrt(1-(("R"-"a")/"R")^2))`

Explanation:

Given: Mass of cylinder is M, radius of cylinder is R, height of the step is a(a < R).

To find: F, the minimum value of force required to pull the cylinder over the step.

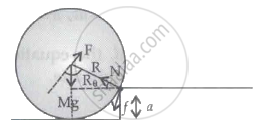
From the above figure, the minimum force required to pull the cylinder over step a is :

F > Mg cos θ

F > Mg `sqrt("R"^2-("R"-"a")^2/"R")`

F > Mg `sqrt(1-(("R"-"a")/"R")^2)`