Question

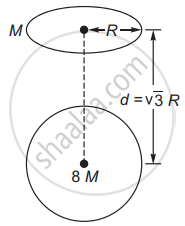
A uniform ring of mass M and radius r is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d = `sqrt3​`R from the centre of the sphere. The gravitational attraction between the sphere and the ring is ______.

विकल्प

• `"GM"/"R"^2`

• `(3"GM"^2)/(2"R"^2)`

• `(2"GM"^2)/(sqrt2"R"^2)`

• `(sqrt3"GM"^2)/("R"^2)`

Answer 1

A uniform ring of mass M and radius r is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d = `sqrt3​`R from the centre of the sphere. The gravitational attraction between the sphere and the ring is `underlinebb((sqrt3"GM"^2)/("R"^2))`.

Explanation:

From the figure, the gravitational intensity due to the ring at a distance d = `sqrt3​`R on its axis is

I = `"GM"/(("d"^2+"R"^2)^(3//2))`

= `("GM"xxsqrt3"R")/((3"R"^2+"R"^2)^(3//2))`

= `(sqrt3"GM")/(8"R"^2)`

Force on sphere = (8M)I = (8M) × `(sqrt3"M")/(8"R"^2)`

= `(sqrt3"GM"^2)/("R"^2)`