Advertisements
Advertisements
प्रश्न
A uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the centre
विकल्प
is maximum when h = 0
is maximum when h = R
is maximum when h = 2R
is independent of h.
उत्तर
is independent of h. 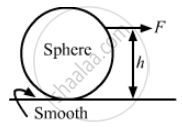
As the uniform sphere is placed on a smooth surface, the sphere only slips. The acceleration of the centre of the sphere is given by,
\[\frac{\text{ Applied force}}{\text{ Mass of the sphere }}\] ,which is independent of height h.
APPEARS IN
संबंधित प्रश्न
What can be said about the centre of mass of a uniform hemisphere without making any calculation? Will its distance from the centre be more than r/2 or less than r/2?
A heavy ring of mass m is clamped on the periphery of al light circular disc. A small particle having equal mass is clamped at the centre of the disc. The system is rotated in such a way that the centre moves in a circle of radius r with a uniform speed v. We conclude that an external force
A uniform disc of radius R is put over another uniform disc of radius 2R of the same thickness and density. The peripheries of the two discs touch each other. Locate the centre of mass of the system.
One end of a uniform rod of mass m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity \[\omega\] The force exerted by the clamp on the rod has a horizontal component
A uniform rod is kept vertically on a horizontal smooth surface at a point O. If it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain _________ .
A uniform chain of mass M and length L is held vertically in such a way that its lower end just touches the horizontal floor. The chain is released from rest in this position. Any portion that strikes the floor comes to test. Assuming that the chain does not form a heap on the floor calculate the force exerted by it on the floor when a length x has reached the floor.
A rod of mass m and length L, lying horizontally, is free to rotate about a vertical axis through its centre. A horizontal force of constant magnitude F acts on the rod at a distance of L/4 from the centre. The force is always perpendicular to the rod. Find the angle rotated by the rod during the time t after the motion starts.
A square plate of mass 120 g and edge 5⋅0 cm rotates about one of the edges. If it has a uniform angular acceleration of 0⋅2 rad/s2 what torque acts on the plate?
Calculate the torque on the square plate of the previous problem if it rotates about a diagonal with the same angular acceleration.
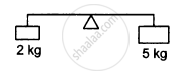
A light rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the following figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.
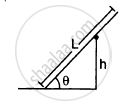
A uniform rod of length L rests against a smooth roller as shown in the following figure. Find the friction coefficient between the ground and the lower end if the minimum angle that the rod can make the horizontal is θ.
A uniform rod of length L lies on a smooth horizontal table. A particle moving on the table strikes the rod perpendicularly at an end and stops. Find the distance travelled by the centre of the rod by the time it turns through a right angle. Show that if the mass of the rod is four times that of the particle, the collision is elastic.
