Question

A wire of length 36 m is cut into two pieces, one of the pieces is bent to form a square and the other is bent to form a circle. If the sum of the areas of the two figures is minimum, and the circumference of the circle is k (meter), then `(4/π + 1)`k is equal to ______.

विकल्प

• 34

• 35

• 36

• 37

Answer 1

A wire of length 36 m is cut into two pieces, one of the pieces is bent to form a square and the other is bent to form a circle. If the sum of the areas of the two figures is minimum, and the circumference of the circle is k (meter), then `(4/π + 1)`k is equal to 36.

Explanation:

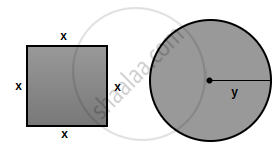
4x + 2πy = 36  (given)  ...(1)

Area = x² + πy²

A = `x^2 + 1/π(18 - 2x)^2` ......Using equation (i)

Differentiating w.r.t.x

`("dA")/("d"x) = 2x + 2/π(18 - 2x)(-2)`

`("dA")/("d"x) = (2πx + (36 - 4x)(-2))/π`

For maxima and minima,

`("dA")/("d"x)` = 0

⇒ 2πx – 72 + 8x = 0

⇒ x = `36/(π + 4)`

⇒ `("d"^2"A")/("d"x^2) > 0`

⇒ y = `18/(π + 4)`  ......Using equation (i)

k[circumference of circle] = 2πy

⇒ k = `(36π)/(π + 4)`

∴ Value of `((4 + π)/π) xx "k"` = 36