Advertisements
Advertisements
प्रश्न
एका त्रिकोणाचा पाया 9 आणि उंची 5 आहे. दुसऱ्या त्रिकोणाचा पाया 10 आणि उंची 6 आहे, तर त्या त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर काढा.
उत्तर
समजा, पहिल्या त्रिकोणाचे पाया, उंची व क्षेत्रफळ अनुक्रमे b1, h1 आणि A1 आहेत. दुसऱ्या त्रिकोणाचे पाया, उंची व क्षेत्रफळ अनुक्रमे b2, h2 आणि A2 आहेत.
`"A"_1/"A"_2 = ("b"_1 xx "h"_1)/("b"_2 xx "h"_2)` .............[दोन त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर हे त्यांच्या पाया व संगत उंची यांच्या गुणाकारांच्या गुणोत्तराएवढे असते.]
`"A"_1/"A"_2 = (9 xx 5)/(10 xx 6) = 45/60`
∴ `"A"_1/"A"_2 = 3/4`
∴ त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर 3 : 4 आहे.
APPEARS IN
संबंधित प्रश्न
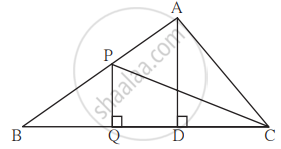
दिलेल्या आकृतीत, PQ ⊥ BC, AD ⊥ BC तर खालील गुणोत्तरे लिहा.
i) `"A(ΔPQB)"/"A(ΔPBC)"`
ii) `"A(ΔPBC)"/"A(ΔABC)"`
iii) `"A(ΔABC)"/"A(ΔADC)"`
iv) `"A(ΔADC)"/"A(ΔPQC)"`
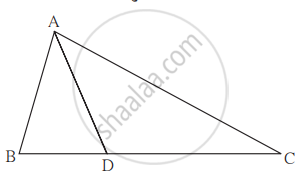
ΔABC मध्ये B - D – C आणि BD = 7, BC = 20 तर खालील गुणोत्तरे काढा.
- `("A"(Δ"ABD"))/("A"(Δ"ADC"))`
- `("A"(Δ"ABD"))/("A"(Δ"ABC"))`
- `("A"(Δ"ADC"))/("A"(Δ"ABC"))`
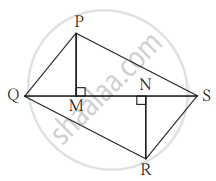
आकृती मध्ये PM = 10 सेमी A(ΔPQS) = 100 चौसेमी A(ΔQRS) = 110 चौसेमी तर NR काढा.
जर ∆XYZ ~ ∆PQR, तर `"XY"/"PQ" = "YZ"/"QR"` = ?
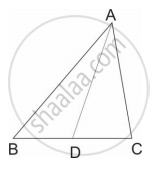
आकृतीमध्ये BD = 8, BC = 12 B-D-C, तर `("A"(Delta"ABC"))/("A"(Delta"ABD"))` = ?
∆ABC ~ ∆DEF, तर प्रमाणात असणाऱ्या संगत बाजू लिहा.
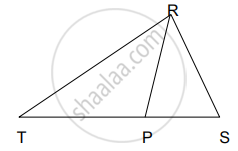
आकृतीमध्ये TP = 10 सेमी, PS = 6 सेमी. `("A"(Delta"RTP"))/("A"(Delta"RPS"))` = ?
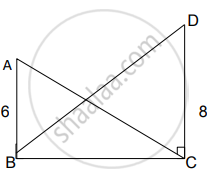
आकृतीमध्ये, दिलेल्या माहितीवरून ∠ABC = 90°, ∠DCB = 90°, AB = 6, DC = 8, तर `("A"(Delta"ABC"))/("A"(Delta"BCD"))` किती?
∆ABC मध्ये, B-D-C आणि BD = 7, BC = 20, तर खालील गुणोत्तर काढा.
`("A"(Delta"ABD"))/("A"(Delta"ADC"))`
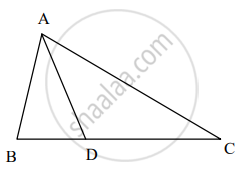
∆ABC मध्ये, B-D-C आणि BD = 7, BC = 20, तर खालील गुणोत्तर काढा.

`(A(∆ABD))/(A(∆ABC))`
