Advertisements
Advertisements
प्रश्न
आकृती मध्ये दिलेल्या माहितीवरून AB आणि BC काढण्यासाठी खालील कृती पूर्ण करा.

AB = BC ...........`square`
∴ ∠BAC = `square`
∴ AB = BC = `square` × AC
= `square xx sqrt(8)`
= `square xx 2sqrt(2)`
= `square`
उत्तर
AB = BC .....[पक्ष]
∴ ∠BAC = ∠BCA ....[समद्विभुज त्रिकोणाचे प्रमेय]
समजा, ∠BAC = ∠BCA = x .....(i)
ΔABC मध्ये,
∠A + ∠B + ∠C = 180° ........[त्रिकोणाच्या तिन्ही कोनांच्या मापांची बेरीज 180° असते.]
∴ x + 90° + x = 180° .....[(i) वरून]
∴ 2x = 90°
∴ x = `90^circ/2` .....[(i) वरून]
∴ x = 45°
∴ ∠BAC = ∠BCA = 45°
∴ ΔABC हा 45° - 45° - 90° त्रिकोण आहे.
∴ AB = BC = `1/sqrt2` × AC ...[45° कोनासमोरील बाजू]
= `1/sqrt2 xx sqrt(8)`
= `1/sqrt2 xx 2sqrt(2)`
∴ AB = BC = 2 एकक
APPEARS IN
संबंधित प्रश्न
एका चौरसाचा कर्ण `10sqrt2` सेमी असल्यास त्याची परिमिती ______ असेल.
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका चौरसाचा कर्ण `10sqrt2` सेमी असल्यास त्याची परिमिती ______ असेल.
सोबतच्या आकृतीत, ∆ABC मध्ये, AB = BC, AC = 5`sqrt2`, AB ⊥ BC, तर ABC ची उंची किती?
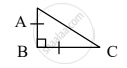
सोबतच्या आकृतीत, ∆MNK मध्ये, ∠MNK = 90°, ∠M = 45° MK = 6, तर MN व KN काढण्यासाठी खालील कृती पूर्ण करा.
कृती: ∆MNK मध्ये,
∠MNK = 90°, ∠M = 45° ……[पक्ष]
∴ ∠K = `square`.... [∆MNK च्या उरलेल्या कोनाचे माप],
∆MNK हा 45° – 45° – 90° त्रिकोण आहे,
45° – 45° – 90° त्रिकोणाच्या प्रमेयानुसार,
`square = 1/sqrt2"MK"` व `square = 1/sqrt2"MK".`
∴ MN = `1/sqrt2 xx square` व KN = `1/sqrt2 xx 6`
∴ MN = `3sqrt2` व KN = `3sqrt2`
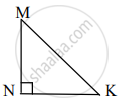
सोबतच्या आकृतीत, ∆ABC मध्ये, AD ⊥ BC, ∠C = 45° AC = `8sqrt2` BD = 5, तर AD व BC काढण्यासाठी खालील कृती पूर्ण करा.
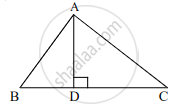
कृती: ∆ADC मध्ये,
∠ADC = 90°, ∠C = 45° …....[पक्ष]
∴ ∠DAC = `square` ........[∆ADC च्या उरलेल्या कोनाचे माप],
∆ADC हा 45° – 45° – 90° त्रिकोण आहे,
45° – 45° – 90° त्रिकोणाच्या प्रमेयानुसार,
`square = 1/sqrt2"AC"` व `square = 1/sqrt2"AC"`
∴ AD = `1/sqrt2 xx square` व DC = `1/sqrt2 xx 8sqrt2`
∴ AD = `1/sqrt2 xx 8sqrt2` व DC = `1/sqrt2 xx 8sqrt2`
∴ AD = 8 व DC = 8
BC = BD + DC = 5 + 8 = 13
ΔABC मध्ये ∠ABC = 90°, ∠BAC = ∠BCA = 45°. जर AC = `9sqrt(2)` असेल, तर AB ची किंमत काढा.

