Advertisements
Advertisements
प्रश्न
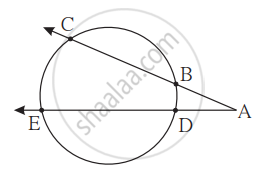
आकृती मध्ये, m(कंस CE) = 54°, m(कंस BD) = 23°, तर ∠CAE = किती?
उत्तर
जीवा BC व ED एकमेकांना वर्तुळाच्या बाह्यभागात A बिंदूत छेदतात.
∴ ∠CAE = `1/2`[m(कंस CE) - m(कंस BD)]
= `1/2(54^circ - 23^circ) = 1/2 xx 31^circ`
∴ ∠CAE = 15.5°
APPEARS IN
संबंधित प्रश्न
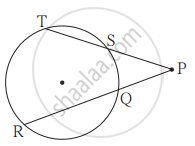
आकृती मध्ये, जर PQ = 6, QR = 10, PS = 8 तर TS = किती?
प्रत्येक उपप्रश्नासाठी चार पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक पर्याय निवडा.
एकाच वर्तुळावर बिंदू A, B, C असे आहेत, की m(कंस AB) = m(कंस BC) = 120°, दोन्ही कंसात B शिवाय एकही बिंदू सामाईक नाही. तर ΔABC कोणत्या प्रकारचा आहे?
आकृती मध्ये, AB = 4.2, BC = 5.4, AE = 12.0 तर AD = किती?

आकृती मध्ये, AB = 3.6, AC = 9.0, AD = 5.4 तर AE = किती?

आकृतीमध्ये, जीवा PQ आणि जीवा RS एकमेकींना बिंदू T मध्ये छेदतात, तर m∠STQ = `1/2`m(कंस PR) + m(कंस SQ)] हे सिद्ध करण्यासाठी खालील चौकटी भरून कृती पूर्ण करा.
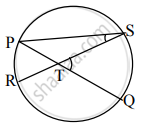
सिद्धता:
m∠STQ = m∠SPQ + `square` .....[त्रिकोणाच्या बाह्य कोनाचे प्रमेय]
= `1/2`m(कंस SQ) + `square` ..........[अंतर्लिखित कोनाचे प्रमेय]
= `1/2[square + square]`
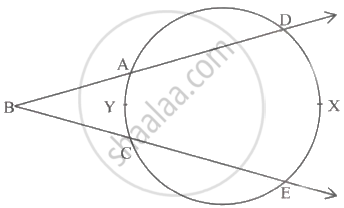
वरील आकृतीत, m(कंस DXE) = 105°, m(कंस AYC) = 47°, तर ∠DBE चे माप काढा.
