Advertisements
Advertisements
प्रश्न
AB and AC are the two chords of a circle whose radius is r. If p and q are
the distance of chord AB and CD, from the centre respectively and if
AB = 2AC then proove that 4q2 = p2 + 3r2.
उत्तर
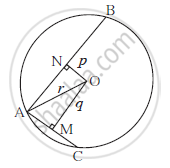
Let AC = a then AB = 2a
seg OM ⊥ chord AC, seg ON ⊥ chord AB.
AM =MC = `a/2` and AN = NB = a
In Δ OMA and Δ ONA, By theorem of Pythagoras,
`AO^2 = AM^2 + MO^2`
`AO^2 = AN^2+ q^2` ....... (1)
`AO^2 = AN^2 + NO^2`
`AO^2 = a^2 + p^2` ........ (2)
From equation (1) and (2)
`(a/2)^2 + q^2 = a^2 + p^2`
`a^2/4 + q^2 = a^2 + p^2`
`a^2 + 4q^2 = 4a^2 + 4p^2`
`4q^2 = 3a^2 + 4p^2`
`4q^2 = p^2 + 3(a^2 + p^2)`
`4q^2 = p^2 + 3r^2 .... ("In" Δ ONA, r^2 = a^2 + p^2)`
APPEARS IN
संबंधित प्रश्न
If the point (x, y) is equidistant from the points (a + b, b – a) and (a – b, a + b), prove that bx = ay
If P and Q are two points whose coordinates are (at2 ,2at) and (a/t2 , 2a/t) respectively and S is the point (a, 0). Show that `\frac{1}{SP}+\frac{1}{SQ}` is independent of t.
Find the coordinates of the circumcentre of the triangle whose vertices are (8, 6), (8, – 2) and (2, – 2). Also, find its circum radius
For what values of k are the points (8, 1), (3, –2k) and (k, –5) collinear ?
Find the distances between the following point.
A(a, 0), B(0, a)
Find the distance between the following point :
(sec θ , tan θ) and (- tan θ , sec θ)
Find the distance between the following point :
(Sin θ - cosec θ , cos θ - cot θ) and (cos θ - cosec θ , -sin θ - cot θ)
Find the coordinates of O, the centre passing through A( -2, -3), B(-1, 0) and C(7, 6). Also, find its radius.
Prove that the points (1 , 1) , (-1 , -1) and (`- sqrt 3 , sqrt 3`) are the vertices of an equilateral triangle.
Find the distance between the following pairs of points:
`(3/5,2) and (-(1)/(5),1(2)/(5))`
A point P (2, -1) is equidistant from the points (a, 7) and (-3, a). Find a.
The points A (3, 0), B (a, -2) and C (4, -1) are the vertices of triangle ABC right angled at vertex A. Find the value of a.
Find distance between point A(7, 5) and B(2, 5)
The point which lies on the perpendicular bisector of the line segment joining the points A(–2, –5) and B(2, 5) is ______.
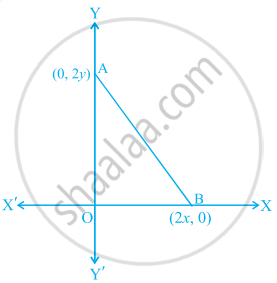
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
The points (– 4, 0), (4, 0), (0, 3) are the vertices of a ______.
∆ABC with vertices A(–2, 0), B(2, 0) and C(0, 2) is similar to ∆DEF with vertices D(–4, 0), E(4, 0) and F(0, 4).
What is the distance of the point (– 5, 4) from the origin?
A point (x, y) is at a distance of 5 units from the origin. How many such points lie in the third quadrant?
