Question

`triangle`ABC या समद्विभुज त्रिकोणात ∠A व ∠B यांची मापे समान आहेत. ∠ACD हा `triangle`ABC चा बाह्यकोन आहे. ∠ACB व ∠ACD ची मापे अनुक्रमे (3x − 17)^° व (8x + 10)^° आहेत, तर ∠ACB व ∠ACD यांची मापे काढा. तसेच ∠A व ∠B यांचीही मापे काढा.

Answer 1

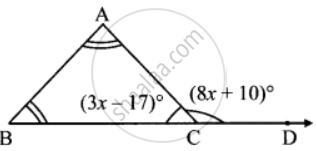
दिलेले:

∠ACB = (3x − 17)^∘

∠ACD = (8x + 10)^∘

आता, ∠ACB + ∠ACD = 180^∘ ...(रेषीय जोडीतील कोन)

⇒ 3x^° − 17^° + 8x^° + 10^° = 180^°

⇒ 3x^° + 8x^° − 17^° + 10^° = 180^°

⇒ 11x^° − 7^° = 180^°

⇒ 11x^° – 7^° + 7^° = 180^° + 7 ...(दोन्ही बाजूंना 7 जोडून)

⇒ 11x^° = 187^°

⇒ x^° = `187^circ/11^circ`

⇒ x^° = 17^°

त्यामुळे,

∠ACB = (3x − 17)^°

= (3 × 17)^° − 17^°

= (51 − 17)^°

= 34^°

∠ACD = (8x + 10)^°

= (8 × 17)^° + 10^°

= (136 + 10)^°

= 146^°

आता, ∠A + ∠B = ∠ACD ...(बाह्य कोन गुणधर्म)

⇒ 2∠A = 146^° (∵∠A = ∠B)

⇒ x^° = `146^circ/2^circ`

⇒ ∠A = 73^°

म्हणून, ∠ACB, ∠ACD, ∠A आणि ∠B चे माप अनुक्रमे 146^°, 34^°, 73^° आणि 73^° आहेत.