Advertisements
Advertisements
प्रश्न
ABCD एक समचतुर्भुज है दर्शाइए कि AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B तथा D दोनों को समद्विभाजित करता है |
उत्तर
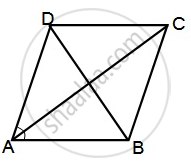
दिया है : ABCD एक समचतुर्भुज चतुर्भुज है |
सिद्ध करना है :
(i) AC, ∠A तथा ∠C को भी समद्विभाजित करता है |
(ii) BD, ∠B तथा ∠D को भी समद्विभाजित करता है |
प्रमाण:
(i) ΔABC तथा ΔADC में,
AB = AD (समचतुर्भुज की भुजाएँ)
∠B = ∠D (समचतुर्भुज के सम्मुख कोण बराबर होते है )
AC = AC (उभयनिष्ठ)
अत: SAS सर्वांगसमता नियम से
ΔABC ≅ ΔADC
∴ ∠BAC = ∠DAC (By CPCT) ................ (1)
∴ ∠BCA = ∠DCA (By CPCT) ................(2)
समीo (1) तथा (2) से
विकर्ण AC, ∠A तथा ∠C को समद्विभाजित करता है |
इसी प्रकार हम
(ii) BD, ∠B तथा ∠D को भी समद्विभाजित करता है |
APPEARS IN
संबंधित प्रश्न
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हो और परस्पर समद्विभाजित करें, तो वह एक वर्ग होता है |
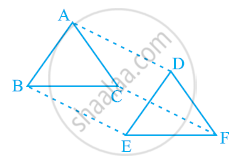
ΔABC और ΔDEF में, AB = DE, AB || DE, BC = EF और BC || EF है | शीर्षों A, B और C को क्रमश: शीर्षों D, E और F से जोड़ा जाता है | दर्शाइए कि
- चतुर्भुज ABED एक समांतर चतुर्भुज है।
- चतुर्भुज BEFC एक समांतर चतुर्भुज है।
- AD || CF और AD = CF है |
- चतुर्भुज ACFD एक समांतर चतुर्भुज है।
- AC = DF है
- Δ ABC ≅ Δ DEF है