Advertisements
Advertisements
प्रश्न
An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km/h. Compare its centripetal acceleration with the acceleration due to gravity.
उत्तर
Radius of the loop, r = 1 km = 1000 m
Speed of the aircraft, `v = 900 "km/h" = 900 xx 5/18 = 250 "m/s"`
Centripetal acceleration, `a_c = v^2/r`
`=(250)^2/1000 = 62.5 "m/s"^2`
Acceleration due to gravity, g = 9.8 m/s2
`a_c/g = 62.5/9.8 = 6.38`
`a_c =6.38 g`
APPEARS IN
संबंधित प्रश्न
Read the statement below carefully and state, with reason, if it is true or false:
The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
A uniform circular motion is an accelerated motion. Explain it. State whether the acceleration is uniform or variable? Name the force responsible to cause this acceleration. What is the direction of force at any instant? Draw a diagram in support of your answer.
Is it possible to have an accelerated motion with a constant speed? Explain.
Solve the following problem.
A projectile is thrown at an angle of 30° to the horizontal. What should be the range of initial velocity (u) so that its range will be between 40m and 50 m? Assume g = 10 m s-2.
A particle goes round a circular path with uniform speed v. After describing half the circle, what is the change in its centripetal acceleration?
A small sphere is attached to a cord and rotates in a vertical circle about a point O. If the average speed of the sphere is increased, the cord is most likely to break at the orientation when the mass is at ____________.
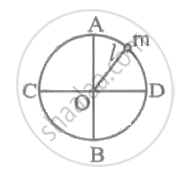
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 8 cm. The centripetal force acting on the particle is 15 N. Its kinetic energy is ____________.
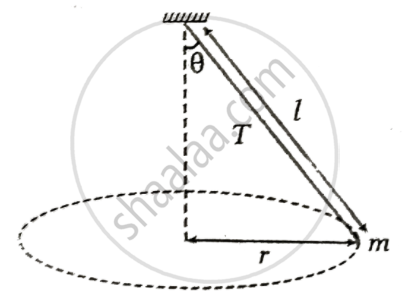
A string of length 'l' fixed at one end carries a mass 'm' at the other end. The string makes `3/pi` revolutions/second around the vertical axis through the fixed end as shown in figure. The tension 'T' in the string is ______.
Define uniform circular motion and give an example of it. Why is it called accelerated motion?
A point object moves along an arc of a circle of radius 'R'. Its velocity depends upon the distance covered 'S' as V = `Ksqrt(S)` where 'K' is a constant. If 'e' is the angle between the total acceleration and tangential acceleration, then
