Question

An arc of a circle of radius 21 cm subtends an angle of 60° at the centre Find: 

1. the length of the arc.
2. the area of the minor segment of the circle made by the corresponding chord.

Answer 1

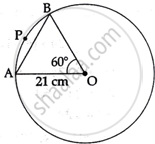
i. Given, r = 21 cm, θ = 60°

length of the arc APB = `theta/(360"°") xx 2pir`

= `(60"°")/(360"°") xx 2 xx 22/7 xx 21`

= `1/6 xx 2 xx 22 xx 3`

= 22 cm

ii. Area of the minor segment = Area of sector OAPB − Area of triangle of OAB

Now, Area of sector APB = `theta/(360"°") xx pir^2`

= `(60"°")/(360"°") xx 22/7 xx (21)^2`

= `1/6 xx 22/7 xx 21 xx 21`

= 231 cm²

and Area of triangle OAB = `1/2` × base × height

= `1/2` AB × OM

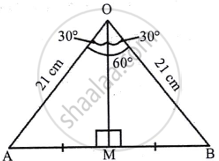
We draw OM ⊥ AB

∴ ∠OMB = ∠OMA = 90°

and by symmetry, M is mid-point of AB

∴ BM = AM = `1/2` AB   ...(i)

In right ΔOMA, sin30° = `(AM)/(AO)`

⇒ `1/2 = (AM)/21`

⇒ AM = `21/2` cm

In right ΔOMA,

cos 30° = `(OM)/(AO)`

⇒ `sqrt3/2 = (OM)/21`

⇒ OM = `sqrt3/2 xx 21` cm

∴ from eq. (i)

AM = `1/2` AB

⇒ AB = 2 AM = `2 xx 21/2 = 21` cm

Thus, Area of ΔOAB = `1/2 xx 21 xx sqrt3/2 xx 21`

= `(441sqrt3)/4` cm²

Therefore, area of minor segment

= `(231 - (441sqrt3)/4)` cm²