Question

An equilateral triangle is inscribed in a circle of radius 6 cm. Find its side.

Answer 1

Let ABC be an equilateral triangle inscribed in a circle of radius 6 cm. Let O be the centre of the circle.

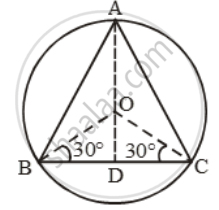
Then, OA = OB = OC = 6 cm.

Let OD be perpendicular from O on side BC. Then, D is mid-point of BC and OB and OC are bisectors of ∠B and ∠C respectively.

∴ ∠OBD = 30°

In ∆OBD, right angled at D, we have

∠OBD = 30° and OB = 6 cm.

`\therefore \cos \angle OBD=\frac{BD}{OB}\Rightarrow \cos60^{0}=\frac{BD}{6}`

`\Rightarrow BD=6\cos 60^{0}=6\times\frac{\sqrt{3}}{2}=3\sqrt{3}\text{ }`

⇒ BC = 2 BD = 2(3√3 )cm = 6 √3 cm.