Advertisements
Advertisements
प्रश्न
An insect is on the 0 point of a number line, hopping towards 1. She covers half the distance from her current location to 1 with each hop. So, she will be at `1/2` after one hop, `3/4` after two hops, and so on.
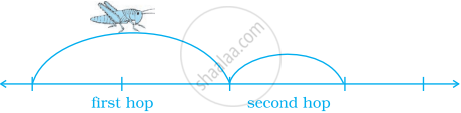
- Make a table showing the insect’s location for the first 10 hops.
- Where will the insect be after n hops?
- Will the insect ever get to 1? Explain.
उत्तर
a. On the basis of given information in the question, we can arrange the following table which shows the insect’s location for the first 10 hops.
| Number of hops | Distance covered | Distance left | Distance covered |
| 1. | `1/2` | `1/2` | `1 - 1/2` |
| 2. | `1/2(1/2) + 1/2` | `1/4` | `1 - 1/4` |
| 3. | `1/2(1/4) + 3/4` | `1/8` | `1 - 1/8` |
| 4. | `1/2(1/8) + 7/8` | `1/16` | `1 - 1/16` |
| 5. | `1/2(1/16) + 15/16` | `1/32` | `1 - 1/32` |
| 6. | `1/2(1/32) + 31/32` | `1/64` | `1 - 1/64` |
| 7. | `1/2(1/64) + 63/64` | `1/128` | `1 - 1/128` |
| 8. | `1/2(1/128) + 127/128` | `1/256` | `1 - 1/256` |
| 9. | `1/2(1/256) + 255/256` | `1/512` | `1 - 1/512` |
| 10. | `1/2(1/512) + 511/512` | `1/1024` | `1 - 1/1024` |
b. If we see the distance covered in each hops
Distance covered in 1st hop = `1 - 1/2`
Distance covered in 2nd hops = `1 - 1/4`
Distance covered in 3rd hops = `1 - 1/8`

Distance covered in n hops = `1 - (1/2)^n`
c. No, because for reaching `1, (1/2)^n` has to be zero for some finite n which is not possible.
APPEARS IN
संबंधित प्रश्न
If y be any non-zero integer, then y0 is equal to ______.
[2–1 + 3–1 + 4–1]0 = ______.
(–4)–4 × (4)–1 = (4)5
Find the value of x–3 if x = (100)1 – 4 ÷ (100)0.
Find a single machine that will do the same job as the given hook-up.
a (× 24) machine followed by `(xx (1/2)^2)` machine.
For hook-up, determine whether there is a single repeater machine that will do the same work. If so, describe or draw it.

For hook-up, determine whether there is a single repeater machine that will do the same work. If so, describe or draw it.
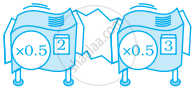
Supply the missing information for diagram.
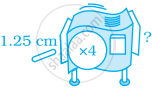
Supply the missing information for diagram.
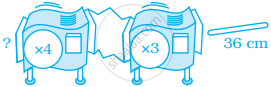
Find x.
23x = 82x + 1
