Advertisements
Advertisements
प्रश्न
Answer in brief:
Derive an expression which relates angular momentum with the angular velocity of a rigid body.
उत्तर
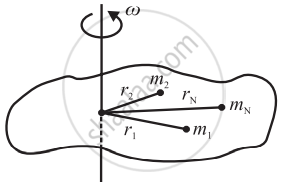
The figure above shows a rigid object rotating with a constant angular speed ω about an axis perpendicular to the plane of paper. For theoretical simplification let us consider the object to be consisting of N number of particles of masses m1, m2, ....., mN at respective perpendicular distances r1, r2,..., rN, respectively from the axis of rotation. As the object rotates, all these particles perform UCM with same angular speed ω , but with different linear speeds `"v"_1=r_1omega`, `"v"_2=r_2omega`, ..., `"v"_N=r_Nomega`.
Directions of individual velocities `vec"v"_1`, `vec"v"_2`, ..., `vec"v"_N` are along the tangents to their respective tracks.
Linear momentum of the first particle is of magnitude
`p_1 = m_1"v"_1= "m"_1"r"_1omega`
Its angular momentum, defined by `vec"L"_1 = vec"p"_1 xx vec"r"_1`, is thus of magnitude
`"L"_1 = "p"_1"r"_1 = "m"_1"r"_1omega"r"_1 = "m"_1"r"_1^2omega`
Similarly, `"L"_2 = "m"_2"r"_2^2omega`, `"L"_3 = "m"_3"r"_3^2omega`, ..., `"L"_N = "m"_N"r"_N^2omega`
The angular momentum of the body about the given axis is
L = `"L"_1 + "L"_2 + ... +"L"_"N"`
`= "m"_1"r"_1^2omega + "m"_2"r"_2^2omega + ...+ "m"_"N""r"_"N"^2 omega`
`= ("m"_1"r"_1^2 + "m"_2"r"_2^2 +... + "m"_"N""r"_"N"^2)omega`
∴ L = Iω
where I = `("m"_1"r"_1^2 + "m"_2"r"_2^2 +... + "m"_"N""r"_"N"^2)` is the moment of inertia of the body about the given axis of rotation.
In vector form, `vec"L" = "I"vecomega`
Thus, angular momentum = moment of inertia × angular velocity.
संबंधित प्रश्न
State and prove: Law of conservation of angular momentum.
The angular momentum of a system of particles is conserved ______
Obtain an expression for the angular momentum of a body rotating with uniform angular velocity.
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity `omega`. Two objects of mass m are attached gently to the opposite ends of diameter of the ring. The wheel will now rotate with angular velocity ______.
If the radius of earth contracts to half of its value today, (the mass remaining unchanged), then the duration of the day will be ____________.
A ceiling fan having a moment of inertia 2 kg-m2 attains its maximum frequency of 60 rpm in ‘2π’ seconds. Calculate its power rating.
Which physical quantity of an atomic electron has the dimensions same as that of h?
