Question

By what number should each of the following numbers be multiplied to get a perfect square ? Also, find the number whose square is the new number. 

8820

 

Answer 1

Factorising number. 

 8820 = 2 x 2 x 3 x 3 x 5 x 7 x 7 

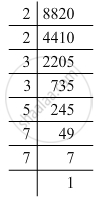
Grouping them into pairs of equal factors:
8820 = (2 x 2) x (3 x 3) x (7 x 7) x 5
The factor, 5 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 8820 must be multiplied by 5 for it to be a perfect square.
The new number would be (2 x 2) x (3 x 3) x (7 x 7) x (5 x 5).
Furthermore, we have:
(2 x 2) x (3 x 3) x (7 x 7) x (5 x 5) = (2 x 3 x 5 x 7) x (2 x 3 x 5 x 7)
Hence, the number whose square is the new number is:
2 x 3 x 5 x 7 = 210