Question

A screen is placed at a distance of 100 cm from an object. The image of the object is formed on the screen by a convex lens for two different locations of the lens separated by 20 cm. Calculate the focal length of the lens used.

Answer 1

 

The distance between the object and the screen (image) is 100 cm.

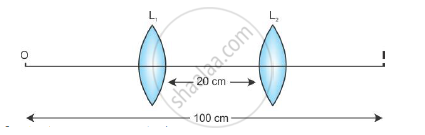
Now, for the first position of the lens:

u = u

v = 100 - u

∴ `1/f=1/(100-u)-1/(-u)=1/(100-u)+1/u`

Now, for the second position of the lens:

u = u + 20

v = 100 - u - 20

`:.1/f=1/(80-u)-1/-(u+20)=1/(80-u)+1/(u+20) `

Therefore, from equations (1) and (2), we get

`1/(100-u)+1/u=1/(80-u)+1/(u+20)`

 `:.1/(100-u)-1/(80-u)=1/(u+20)-1/u`

`:.(80-u-100+u)/((100-u)(80-u))=(u-u-20)/(u(u+20))`

 `:.(-20)/((100-u)(80-u))=(-20)/(u(u+20))`

∴ u(u+20) = (100-u)(80-u)

∴ u² + 20u = 8000 - 180u + u²

∴ 200u = 8000

∴  u = 40 cm

∴ v = 100 - u= 100 - 40 = 60 cm

Therefore, from the lens formula

`1/f=1/v-1/u=1/60-1/(-40)=1/60+1/40`

`:.1/f = (2+3)/120=5/120`

∴ f = 24 cm