Advertisements
Advertisements
प्रश्न
Calculate the area bounded by the parabola y2 = 4ax and its latus rectum
उत्तर
Given parabola is y2 = 4ax
Its focus is (a, 0)
Equation of latus rectum is x = a
The parabola is symmetrical about the x-axis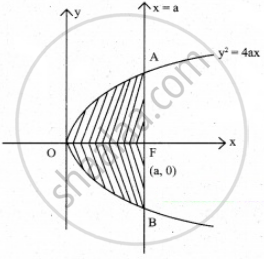
Required area = OAB
= `2 xx int_0^"a" y d"x`
= `2 xx int_0^"a" 2sqrt("a")sqrt(x) "d"x`
= ` sqrt("a") int_0^"a" 2(x)^(1/2) "d"x`
= `4sqrt("a") [(x)^(1/2 + 1)/(1/2 + 1)]_0^"a"`
= `4sqrt("a") [(x)^(3/2)/(3/2)]_0^"a"`
= `4 sqrt("a") xx 2/3 [(x)^(3/2)]_0^"a"`
= `8/3 sqrt("a") [("a")^(3/2) - 0]`
= `8/3 sqrt("a")["a"sqrt("a")]`
= `8/3 "a"^2` sq.units
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the lines y – 2x – 4 = 0, y = 0, y = 3 and the y-axis
Find the area bounded by the line y = x and x-axis and the ordinates x = 1, x = 2
Using integration, find the area of the region bounded by the line y – 1 = x, the x-axis and the ordinates x = – 2, x = 3
Find the area of the region lying in the first quadrant bounded by the region y = 4x2, x = 0, y = 0 and y = 4
Choose the correct alternative:
Area bounded by the curve y = e–2x between the limits 0 ≤ x ≤ `oo` is
Choose the correct alternative:
Area bounded by y = x between the lines y = 1, y = 2 with y-axis is
Choose the correct alternative:
Area bounded by y = ex between the limits 0 to 1 is
Choose the correct alternative:
The area bounded by the parabola y2 = 4x bounded by its latus rectum is
Find the area of the region bounded by the curve between the parabola y = 8x2 – 4x + 6 the y-axis and the ordinate at x = 2
Find the area of the region bounded by the curve y2 = 27x3 and the lines x = 0, y = 1 and y = 2
