Advertisements
Advertisements
प्रश्न
Can a polyhedron have V = F = 9 and E = 16? If yes, draw its figure.
उत्तर
Given, Vertices = 9, Face = 9 and Edges = 16
Using Euler's formula for polyhedron,
F + V – E = 2 ...[Where, F = faces, V = vertices and E = edges]
⇒ 9 + 9 – 16 = 2
⇒ 18 – 16 = 2
⇒ 2 = 2
Hence, the given values satisfies the Euler's formula.
So, a polyhedron can have V = F = 9 and E = 16.
Thus, we can draw a octagonal pyramid.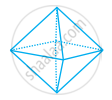
APPEARS IN
संबंधित प्रश्न
Verify Euler’s formula for the following three-dimensional figures:

If the sum of number of vertices and faces in a polyhedron is 14, then the number of edges in that shape is ______.
A polyhedron can have 10 faces, 20 edges and 15 vertices.
Complete the table given below:
| S.No | Solid | Shape of Solid |
Number of faces F |
Number of Verticles V |
Number of edges E |
F + V | E + 2 |
| a. | Cuboid |  |
|||||
| b. | Triangular Pyramid |
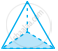 |
|||||
| c. | Square Pyramid |
 |
|||||
| d. | Rectangular Pyramid |
 |
|||||
| e. | Pentagonal Pyramid |
 |
|||||
| f. | Hexagonal Pyramid |
 |
|||||
| g. | Triangular Prism |
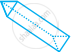 |
|||||
| h. | Square Prism |
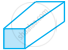 |
|||||
| i. | Cube |  |
|||||
| j. | Pentagonal Prism |
 |
|||||
| k. | Octagonal Prism |
 |
|||||
| l. | Heptagonal Prism |
 |
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.

Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
Using Euler’s formula, find the value of unknown x in the following table.
| Faces | 7 |
| Vertices | 10 |
| Edges | x |
A polyhedron has 20 faces and 12 vertices. Find the edges of the polyhedron.
A solid has forty faces and sixty edges. Find the number of vertices of the solid.
