Question

Complete the following activity to prove that the sum of squares of diagonals of a rhombus is equal to the sum of the squares of the sides.

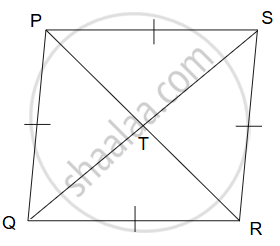
Given:

`square` PQRS is a rhombus. Diagonals PR and SQ intersect each other at point Т.

To prove: PS² + SR² + QR² + PQ² = PR² + QS²

Activity:

Diagonals of a rhombus bisect each other.

In ΔPQS, PT is the median, and in ΔQRS, RT is the median.

∴ By Apollonius theorem,

PQ² + PS² = `square` + 2QT²  ...(I)

QR² + SR² = `square` + 2QT² ...(II)

Adding (I) and (II),

PQ² + PS² + QR² + SR² = 2(PT² + `square`) + 4QT²

= 2(PT² + `square`) + 4QT²  ...(RT = PT)

= 4PT² + 4QT²

= (`square`)² + (2QT)²

∴ PQ² + PS² + QR² + SR² = PR² + `square`

Answer 1

Given:

`square` PQRS is a rhombus. Diagonals PR and SQ intersect each other at point Т.

To prove: PS² + SR² + QR² + PQ² = PR² + QS²

Activity:

Diagonals of a rhombus bisect each other.

In ΔPQS, PT is the median, and in ΔQRS, RT is the median.

∴ By Apollonius theorem,

PQ² + PS² = \[\boxed{2\text{PT}^2}\] + 2QT²  ...(I)

QR² + SR² = \[\boxed{2\text{RT}^2}\] + 2QT² ...(II)

Adding (I) and (II),

PQ² + PS² + QR² + SR² = \[{2(\text{PT}^2 + \boxed{\text{RT}^2})}\] + 4QT²

= \[{2(\text{PT}^2 + \boxed{\text{PT}^2})}\] + 4QT² ...(RT = PT)

= 4PT² + 4QT²

= \[\boxed{(2\text{PT)}^2}\] + (2QT)²

∴ PQ² + PS² + QR² + SR² = PR² + \[\boxed{\text{QS}^2}\]