Advertisements
Advertisements
प्रश्न
Construct an equilateral triangle, given its side and justify the construction.
उत्तर
Let us draw an equilateral triangle of side 5 cm. We know that all sides of an equilateral triangle are equal. Therefore, all sides of the equilateral triangle will be 5 cm. We also know that each angle of an equilateral triangle is 60º.
The below given steps will be followed to draw an equilateral triangle of 5 cm side.
Step I: Draw a line segment AB of 5 cm length. Draw an arc of some radius, while taking A as its centre. Let it intersect AB at P.
Step II: Taking P as centre, draw an arc to intersect the previous arc at E. Join AE.
Step III: Taking A as centre, draw an arc of 5 cm radius, which intersects extended line segment AE at C. Join AC and BC. ΔABC is the required equilateral triangle of side 5 cm.
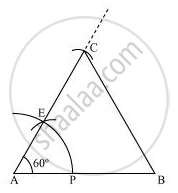
Justification of Construction:
We can justify the construction by showing ABC as an equilateral triangle i.e., AB = BC = AC = 5 cm and ∠A = ∠B = ∠C = 60°.
In ΔABC, we have AC = AB = 5 cm and ∠A = 60°.
Since AC = AB,
∠B = ∠C (Angles opposite to equal sides of a triangle)
In ΔABC,
∠A + ∠B + ∠C = 180° (Angle sum property of a triangle)
⇒ 60° + ∠C + ∠C = 180°
⇒ 60° + 2 ∠C = 180°
⇒ 2 ∠C = 180° − 60° = 120°
⇒ ∠C = 60°
∴ ∠B = ∠C = 60°
We have, ∠A = ∠B = ∠C = 60° ... (1)
⇒ ∠A = ∠B and ∠A = ∠C
⇒ BC = AC and BC = AB (Sides opposite to equal angles of a triangle)
⇒ AB = BC = AC = 5 cm ... (2)
From equations (1) and (2), ΔABC is an equilateral triangle.
APPEARS IN
संबंधित प्रश्न
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Draw a circle with centre at point O. Draw its two chords AB and CD such that AB is not
parallel to CD. Draw the perpendicular bisectors of AB and CD. At what point do they
intersect?
7. Draw a line segment AB and by ruler and compasses1 obtain a line segment of length `3/4`AB.
Draw an obtuse angle, Bisect it. Measure each of the angles so obtained.
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Using ruler and compasses only, draw a right angle.
Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Construct the following angles at the initial point of a given ray and justify the construction 45°
Construct the angle of the measurement :
1. 30°
Construct a rhombus whose side is of length 3.4 cm and one of its angles is 45°.
