Advertisements
Advertisements
प्रश्न
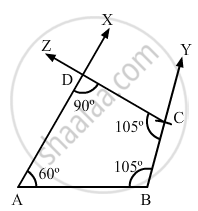
Construct a quadrilateral ABCD, where AB = 5.5 cm, BC = 3.7 cm, ∠A = 60°, ∠B = 105° and ∠D = 90°.
Advertisements
उत्तर
We know that the sum of all the angles in a quadrilateral is 360 .
i . e . , ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠C = 105°
Steps of construction:
Step I: Draw AB = 5 . 5 cm .
Step II: Construct ∠XAB = 60° at A and ∠ABY = 105° .
Step III: With B as the centre and radius 3 . 7 cm, cut off BC = 3 . 7 cm .
Step IV: At C, draw ∠BCZ = 105° such that it meets AX at D .
The quadrilateral so obtained is the required quadrilateral .
APPEARS IN
संबंधित प्रश्न
Construct the following quadrilaterals.
Parallelogram HEAR
HE = 5 cm
EA = 6 cm
∠R = 85°
Construct the following quadrilaterals.
Rectangle OKAY
OK = 7 cm
KA = 5 cm
Construct a quadrilateral ABCD in which AB = 3.8 cm, BC = 3.4 cm, CD = 4.5 cm, AD = 5 cm and ∠B= 80°.
Construct a quadrilateral ABCD in which AB = BC = 3 cm, AD = CD = 5 cm, and ∠B = 120°.
Construct a quadrilateral PQRS, in which PQ = 3.5 cm, QR = 2.5 cm, RS = 4.1 cm, ∠Q = 75° and ∠R = 120°.
Construct a quadrilateral PQRS, in which ∠Q = 45°, ∠R = 90°, QR = 5 cm, PQ = 9 cm and Rs = 7 cm.
Construct a quadrilateral PQRS, where PQ = 3.5 cm, QR = 6.5 cm, ∠P = ∠R = 105° and ∠S = 75°.
Construct a quadrilateral PQRS, in which PQ = 4 cm, QR = 5 cm, ∠P = 50°, ∠Q = 110° and ∠R = 70°.
Construct the following quadrilaterals with the given measurements and also find their area.
AGRI, AG = 4.5 cm, GR = 3.8 cm, ∠A = 60°, ∠G = 110° and ∠R = 90°
______ measurements can determine a quadrilateral uniquely.
