Advertisements
Advertisements
प्रश्न
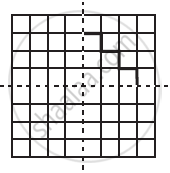
Copy the figure given here.

Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?
उत्तर
We can shade a few more squares so as to make the given figure symmetric about any of its diagonals.
Yes, the figure is symmetric about both the diagonals. There is more than one way so as to make the figure symmetric about a diagonal as we can choose any of its 2 diagonals.

APPEARS IN
संबंधित प्रश्न
Copy the figure with punched holes and find the axes of symmetry for the following:

Given the line of symmetry, find the other hole:
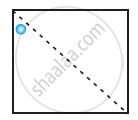
In the given figure, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete given figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
In the given figure, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete given figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
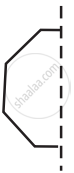
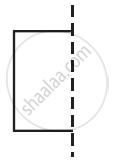
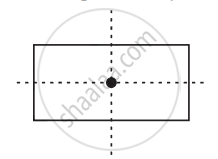
The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
 |
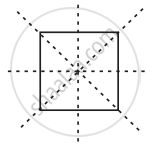 |
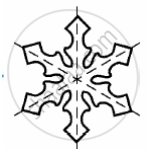 |
| (a) | (b) | (c) |
Identify multiple lines of symmetry, if any, in the following figure.

The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
 |
 |
 |
| (a) | (b) | (c) |
Identify multiple lines of symmetry, if any, in the following figure.
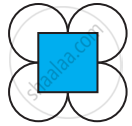
Copy the diagram and complete the given shape to be symmetric about the mirror line(s):
State the number of lines of symmetry for a scalene triangle figure.
State the number of lines of symmetry for a regular hexagon figure.
How many lines of symmetry for the following figure
