Advertisements
Advertisements
प्रश्न
Deduce the expression for the torque `vec"τ"` acting on a planar loop of area `vec"A"` acting on a planar loop of area `vec"B"`. If the loop is free to rotate, what would be its orientation in stable equilibrium?
उत्तर
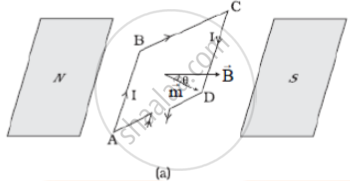
(a) The area vector of the loop ABCD makes an arbitrary angle θ with the magnetic field.
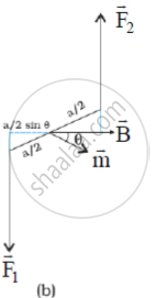
(b) Top view of the loop. The forces F1 and F2 acting on the arms AB and CD are indicated.
We consider the case when the plane of the loop, is not along the magnetic field but makes an angle θ with it. Fig. (a) illustrates this general case. The forces on the arms BC and DA are equal, opposite, and act along the axis of the coil, which connects the centers of mass of BC and DA. Being collinear along the axis they cancel each other, resulting in no net force or torque. The forces on arms AB and CD are F1and F2. They too are equal and opposite, with magnitude,
F1 = F2 = I b B
But they are not collinear! This results in a couple of Fig. (b) is a view of the arrangement from the AD end and it illustrates these two forces constituting a couple. The magnitude of the torque on the loop is,
`"τ" = "F"_1 "a"/(2) sin θ + "F"_2 "a"/(2) sin θ`
= I ab B sin θ
= I A B sin θ ....(i)
As θ → 0, the perpendicular distance between the forces of the couple also approaches zero. This makes the forces collinear and the net force and torque zero. The torques in the above equation can be expressed as vector products of the magnetic moment of the coil and the magnetic field. We define the magnetic moment of the current loop as,
m = I A
where the direction of the area vector A is given by the right-hand thumb rule and is directed into the plane of the paper in Fig. (a). Then as the angle between m and B is `theta`, equation (i) can be expressed by one expression
`vec"τ" = vec"m" xx vec"B"`
we see that the torque `vec"τ" "vanishes when" vec"m"` is either parallel or antiparallel to the magnetic field `vec"B"` This indicates a state of equilibrium as there is no torque on the coil (this also applies to any object with a magnetic moment `vec"m").`
When `vec"m" and vec"B"` re parallel the equilibrium is a stable one.
APPEARS IN
संबंधित प्रश्न
Deduce the expression for the torque acting on a dipole of dipole moment `vecp` in the presence of a uniform electric field `vecE`
An electric dipole with dipole moment 4 × 10−9 C m is aligned at 30° with the direction of a uniform electric field of magnitude 5 × 104 N C−1. Calculate the magnitude of the torque acting on the dipole.
In a certain region of space, electric field is along the z-direction throughout. The magnitude of electric field is, however, not constant but increases uniformly along the positive z-direction, at the rate of 105 NC−1 per metre. What are the force and torque experienced by a system having a total dipole moment equal to 10−7 Cm in the negative z-direction?
An electric dipole is placed in a uniform electric field. The net electric force on the dipole
Maximum torque acting on an electric dipole of moment 3×10-29 Cm in a uniform electric field E is 6 × 10-25 Nm. Find E.
An electric dipole of dipole moment `vecP` is placed in a uniform electric field `vecE` with its axis inclined to the field. Write an expression for the torque `vecT` experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is:
- maximum
- Zero
Answer the following question.
Derive the expression for the torque acting on an electric dipole, when it is held in a uniform electric field. identify the orientation of the dipole in the electric field, in which it attains a stable equilibrium.
A short bar magnet of magnetic moment m = 0.32 J T–1 is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its
- stable, and
- unstable equilibrium?
What is the potential energy of the magnet in each case?
If the solenoid is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of 30° with the direction of applied field?
A circular coil of 16 turns and radius 10 cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 5.0 × 10−2 T. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of 2.0 s−1. What is the moment of inertia of the coil about its axis of rotation?
Assertion: The poles of magnet can not be separated by breaking into two pieces.
Reason: The magnetic moment will be reduced to half when a magnet is broken into two equal pieces.
Let the magnetic field on earth be modelled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator is ______.
An electric dipole of dipole moment 2 × 10-8 C-m in a uniform electric field experiences a maximum torque of 6 × 10-4 N-m. The magnitude of the electric field is ______.
An electric dipole of length 2 cm is placed at an angle of 30° with an electric field 2 × 105 N/C. If the dipole experiences a torque of 8 × 10-3 Nm, the magnitude of either charge of the dipole is ______.
