Question

Derive Bethe’s Law for electron refraction.

Answer 1

Region I has potential V1 and region II has potential V2. The plane surface AB constitutes one of the equipotential surfaces. Let an electron with velocity v1 enter region I making an angle I with the normal. As the electron passes through the equipotential surface AB, it experiences a force which alters its velocity. Because the electric field exists only in the y-direction, the vertical component (y-component) of electron changes while the tangential component (x-component) remains constant.

𝑣1𝑥=𝑣2𝑥

𝑣1sin𝑖=𝑣2sin𝑟

`sin i /sin r=v_2/v_1`

If V1>V2, 𝑣_1𝑦 increases while if V2>V1, _𝑣2𝑦 increases.

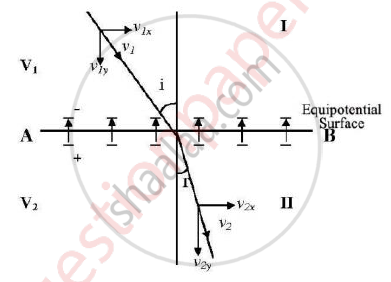
In our case we have taken V2>V1. As the electrons move through the electric field their kinetic energy is provided by the respective potential energy of the electric fields. Hence mv₁²/2=qV₁

And mv₂²/2=qV₂

Dividing the above equation we get,

v1²/ v2²= V₁/ V₂

v₁/ v₂=`sqrt(V1//V2)`

Hence we get,`sin i/sin r=(v2)/(v1)=sqrt((V2)/(V1))`

This is known as Bethe’s law of electron refraction.